 Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
We wtorek, 7 maja 2002 roku, o godzinie 12:45
w sali 304, łącznik A-3-A-4, A G H
Andrzej ŻAK
(WMS, AGH)
wygłosi referat pod tytułem:
Kolorowanie wierzchołków grafu
zbiorami kolorów
W 1976 r. Stahl wprowadził kolorowanie grafu 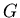 zbiorami
zbiorami 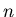 kolorów - tzn. takie przydzielenie
każdemu z wierzchołków kolorów - tzn. takie przydzielenie
każdemu z wierzchołków 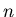 różnych kolorów,
aby sąsiednie wierzchołki nie miały wspólnego koloru.
Liczba różnych kolorów,
aby sąsiednie wierzchołki nie miały wspólnego koloru.
Liczba 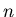 -chromatyczna -chromatyczna 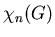 grafu
grafu 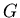 jest najmniejszą liczbą kolorów potrzebnych do
takiego pokolorowania.
Oczywiście, jest najmniejszą liczbą kolorów potrzebnych do
takiego pokolorowania.
Oczywiście,
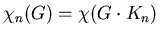 ,
zatem zagadnienie sprowadza się do zwykłego
kolorowania produktu leksykograficznego.
W referacie zostaną opisane pewne własności
liczby ,
zatem zagadnienie sprowadza się do zwykłego
kolorowania produktu leksykograficznego.
W referacie zostaną opisane pewne własności
liczby 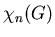 ,
a także konstrukcje przykładów obalających hipotezy
Hajósa i Gellera. ,
a także konstrukcje przykładów obalających hipotezy
Hajósa i Gellera.
|
|
| |
Serdecznie zapraszamy wszystkich chętnych !

