
 Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
We wtorek, 14 maja 2002 roku, o godzinie 12:45
w sali 304, łącznik A-3-A-4, A G H
Gyula Y. KATONA
(Dept. of Comp. Sci. and Inf. Th., Budapest Univ. of Technology)
wygłosi referat pod tytułem:
Hamiltonian chains in hypergraphs
Let 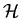 be a be a 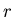 -uniform hypergraph on the vertex set -uniform hypergraph on the vertex set
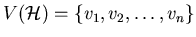 where where 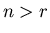 . A cyclic ordering . A cyclic ordering
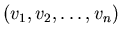 of
the vertex set is called a hamiltonian chain iff for every of
the vertex set is called a hamiltonian chain iff for every
 there exists an edge there exists an edge 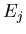 of of 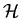 such that such that
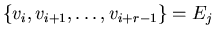 .
An .
An 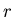 -uniform hypergraph is -uniform hypergraph is 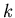 -edge-hamiltonian iff it still contains
a hamiltonian chain after deleting any -edge-hamiltonian iff it still contains
a hamiltonian chain after deleting any 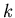 edges of the hypergraph. What
is the minimum
number of edges of such a hypergraph? We give lower and upper bounds for
this question for several values of edges of the hypergraph. What
is the minimum
number of edges of such a hypergraph? We give lower and upper bounds for
this question for several values of 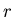 and and 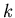 . We also give a
Dirac-type theorem for
the existence of a Hamiltonian chain. . We also give a
Dirac-type theorem for
the existence of a Hamiltonian chain.
|
|
| |
Serdecznie zapraszamy wszystkich chętnych !

