 Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
We wtorek, 8 października 2002 roku, o godzinie 12:45
w sali 304, łącznik A-3-A-4, A G H
Adam Paweł WOJDA
(WMS, AGH)
wygłosi referat pod tytułem:
Cykle i skojarzenia
w grafach dwudzielnych
W 1983 roku K. Berman wykazal następującą hipotezę
Häggkvista z 1979.
Twierdzenie. Jeśli w grafie 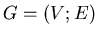 rzędu rzędu
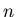 zachodzi zachodzi
to
dowolne skojarzenie w 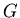 jest zawarte w pewnym cyklu.
Dla cykli hamiltonowskich prawdziwe jest zaś twierdzenie Häggkvista (1979).
Twierdzenie. Jeśli w grafie jest zawarte w pewnym cyklu.
Dla cykli hamiltonowskich prawdziwe jest zaś twierdzenie Häggkvista (1979).
Twierdzenie. Jeśli w grafie 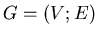 rzędu rzędu 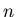 zachodzi
zachodzi
to
dowolne skojarzenie w 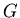 jest zawarte w pewnym cyklu Hamiltona tego grafu.
(Powyższą wersję twierdzenia Häggkvista, nieco ostrzejszą niż oryginalna
wykazalem w 1988.)
W moim referacie przedstawię częściowo
udaną próbę Amar, Flandrin, Gancarzewicza i moją znalezienia odpowiedników
tych wyników dla grafów dwudzielnych. jest zawarte w pewnym cyklu Hamiltona tego grafu.
(Powyższą wersję twierdzenia Häggkvista, nieco ostrzejszą niż oryginalna
wykazalem w 1988.)
W moim referacie przedstawię częściowo
udaną próbę Amar, Flandrin, Gancarzewicza i moją znalezienia odpowiedników
tych wyników dla grafów dwudzielnych.
|
|
| |
Serdecznie zapraszamy wszystkich chętnych !

