 Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
We wtorek, 22 października 2002 roku, o godzinie 12:45
w sali 304, łącznik A-3-A-4, A G H
Anna RYCERZ
(WMS, AGH)
wygłosi referat pod tytułem:
Problem Frobeniusa
a programowanie całkowito-liczbowe
Wiadomo, ze jeśli
sa dodatnimi, wzglednie pierwszymi liczbami całkowitymi, to
istnieje największa dodatnia liczba całkowita 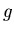 taka, że równanie taka, że równanie
nie ma nieujemnego rozwiązania całkowitego
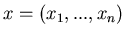 . Problem
określenia . Problem
określenia 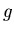 , to problem Frobeniusa. Dla , to problem Frobeniusa. Dla 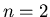
Tematem referatu jest przedstawienie wyniku Vizváriego, który podaje
związek pomiędzy problemem Frobeniusa i programowaniem całkowitoliczbowym.
Użycie metody płaszczyzn odcinających pozwoliło mu podać dolne ograniczenie
na liczbę 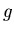 . .
|
|
| |
Serdecznie zapraszamy wszystkich chętnych !

