 Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
We wtorek, 11 marca 2003 roku, o godzinie 12:45
w sali 304, łącznik A-3-A-4, A G H
Gabiel SEMANIŠIN
(Uniwersytet Szafarika, Koszyce)
wygłosi referat pod tytułem:
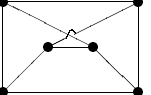
Non-traceable detour graphs
The detour order of a vertex 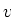 in a graph in a graph 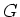 is the length of the
longest path beginning at is the length of the
longest path beginning at 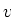 . The detour sequence of . The detour sequence of 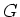 is the
sequence of the detour orders of its vertices. The set of detour orders of
the vertices of is the
sequence of the detour orders of its vertices. The set of detour orders of
the vertices of 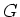 is called detour spectrum of is called detour spectrum of 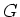 .
A graph is called detour if its detour spectrum is one-element set.
We deal with the problem of existence of a graph with a
prescribed detour sequence .
A graph is called detour if its detour spectrum is one-element set.
We deal with the problem of existence of a graph with a
prescribed detour sequence 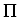 . Particularly, we concentrate on the existence of detour graphs.
The detour deficiency of a graph . Particularly, we concentrate on the existence of detour graphs.
The detour deficiency of a graph 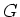 is the difference between the order of is the difference between the order of 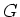 and its detour order.
We show that for every positive integers and its detour order.
We show that for every positive integers 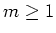 and and 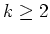 there is a
non-traceable detour graphs with chromatic number there is a
non-traceable detour graphs with chromatic number 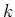 and the
detour deficiency at least and the
detour deficiency at least 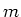 . This answers the question on the existence of non-traceable bipartite detour graphs formulated by F. Bullock. . This answers the question on the existence of non-traceable bipartite detour graphs formulated by F. Bullock.
|
|
| |
Serdecznie zapraszamy wszystkich chętnych !

