Hopfield Network
Hopfield Network is an example of the network with
feedback (so-called recurrent network), where outputs of neurons are connected to input of
every neuron by means of the appropriate weights. Of course there are also inputs which
provide neurons with components of test vector.

In the event of the net that work as
autoassociative memory (our case) weights which connect neuron output with its
input are zeros and the matrix of weights W is symmetrical.
The activation
function of a single neuron looks as follows:

where i and j means index of neurons in N-neural
Hopfield Network, and k is a time
moment. It is very important, that components of x vector are copied to the outputs of neurons in the moment k=0
, and they are disconnected for k>0 (x=0).
In the
recovery mode weights of netowrk connections are constant. The network
„remembers” the pattern vectors, which has been taught, thanks to the weights
of connections. When the network associate input test vector with the pattern
vector their outputs of achieve stable state. It means that input vector is similar to
the one of the pattern vectors.
The network is not able to assign input vector to the any of pattern vectors when
the outputs cannot achieve stable state
In the training mode the weights are calculated on the base of the teaching (pattern) vectors. The simplest teaching method, which is used by us, is the Hebb Rule. Weights are calculated using formula:
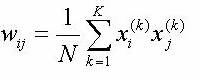
where k means index of teaching vector and K the number of all teaching vectors.
Description of the simulation:
In our
example we recognize 9-pixel picture with the 9-neuron neural network. Black
pixel is represented by 1 and white is represented by -1.In this way we obtained test vectors that have 9 components. Using the Hebb
rule we have taught the network 3 shapes. Two of them remind a circle and a cross:


and the third one is clear picture which is
the vector that consists only -1.
X(1)=[1,1,1,1,-1,1,1,1,1]
X(2)=[1,-1,1,-1,1,-1,1,-1,1]
X(3)=[-1,-1,-1,-1,-1,-1,-1,-1,-1]
e.g. w12= w21= [1*1+1*(-1)+(-1)*(-1)]/9=1/9=0.111111
.
.
.
Complete matrix of weights is presented in
table:
|
|
Neuron 1 |
Neuron 2 |
Neuron 3 |
Neuron 4 |
Neuron 5 |
Neuron 6 |
Neuron 7 |
Neuron 8 |
Neuron 9 |
|
Neuron 1 |
0 |
0.111111 |
0.333333 |
0.111111 |
0.111111 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
|
Neuron 2 |
0.111111 |
0 |
0.111111 |
0.333333 |
-0.111111 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
|
Neuron 3 |
0.333333 |
0.111111 |
0 |
0.111111 |
0.111111 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
|
Neuron 4 |
0.111111 |
0.333333 |
0.111111 |
0 |
-0.111111 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
|
Neuron 5 |
0.111111 |
-0.111111 |
0.111111 |
-0.111111 |
0 |
-0.111111 |
0.111111 |
-0.111111 |
0.111111 |
|
Neuron 6 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
-0.111111 |
0 |
0.111111 |
0.333333 |
0.111111 |
|
Neuron 7 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
0.111111 |
0.111111 |
0 |
0.111111 |
0.333333 |
|
Neuron 8 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
-0.111111 |
0.333333 |
0.111111 |
0 |
0.111111 |
|
Neuron 9 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
0.111111 |
0.111111 |
0.333333 |
0.111111 |
0 |
The picture, which is presented in simulation mode, shows: input values of the
test vector (they are cleared after assigning to neurons outputs - before the second step), outputs
of weights adders, output values and output values from previous step (the
numbers in squares in column).
When the test vector,
which is passed to input of the network, is identical with one of the pattern vectors, the net
does not change its state. It recognizes also test vectors that are similar to patterns.
Sometimes we can see another feature of Hopfield network – remembering
relations between neighboring pixels without their values. As a result of
network activity we get the picture that is the reversed pattern.
Authors:
Provider: MSc A.Gołda
June 2005