Sieć Hopfielda
Sieć Hopfielda jest przykładem sieci ze sprzężeniem zwrotnym (tzw. sieć rekurencyjna), gdzie wyjścia poszczególnych neuronów są podawane z odpowiednimi wagami na wejścia każdego z neuronów. Oczywiście do każdego neuronu podpięte jest wejście, którym doprowadzana jest odpowiednia składowa wektora testowego.

W przypadku, gdy sieć pracuje jako pamięć autoasocjacyjna (nasz przykład) wagi połączenia wyjścia neuronu z własnym wejściem są zerowane. Wymagane jest także, aby macierz wag W była symetryczna.
Funkcja aktywacji pojedynczego neuronu wygląda następująco:
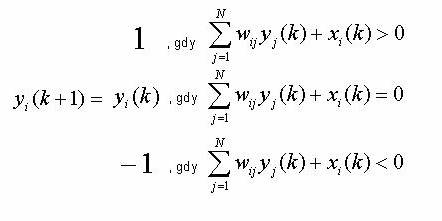
gdzie i oraz j oznaczają numery neuronów N-neuronowej sieci Hopfielda, natomiast k przedstawia chwilę czasową. Należy również zwrócić uwagę na to, że składowe wektora x w chwili czasowej k=0 są przepisywane na wyjścia neuronów, natomiast dla k>0 wejścia są „odpinane” od neuronów (x=0).
W trybie odtwarzania wagi połączeń sieci są ustalone i nie ulegają zmianom. To właśnie dzięki nim sieć „pamięta” wektory wzorcowe, których została „nauczona”. Osiągnięcie na wyjściach sieci stanu ustalonego świadczy, o tym że „skojarzyła” ona wejściowy wektor testowy z „podobnym” do niego wektorem wzorcowym. Jeśli sieć nie dąży do stabilnego wyniku, oznacza to, że nie potrafi ona przyporządkować wektorowi wejściowemu żadnego z zapamiętanych wzorców.
W trybie uczenia, na podstawie zbioru wektorów uczących obliczane są wagi. Najprostszą metodą (wykorzystywaną w naszym przykładzie) uczenia sieci jest reguła Hebb’a. Wagi obliczane są według wzoru:

gdzie k oznacza numer wektora uczącego a K liczbę wszystkich wektorów uczących.
Opis symulacji:
Za pomocą sieci złożonej z 9 neuronów rozpoznajemy obrazek złożony z 9 pikseli. Czarny piksel jest reprezentowany jako 1 natomiast biały jako -1. W ten sposób otrzymaliśmy 9-cioelementowy wektor testowy. Za pomocą reguły Hebb’a „nauczyliśmy” sieć 3 kształtów, z których 2 przypominają kółko i krzyżyk:


a jako trzeci wektor wzorcowy podaliśmy same -1, co odpowiada pustemu kwadratowi.
X(1)=[1,1,1,1,-1,1,1,1,1]
X(2)=[1,-1,1,-1,1,-1,1,-1,1]
X(3)=[-1,-1,-1,-1,-1,-1,-1,-1,-1]
np. w12= w21= [1*1+1*(-1)+(-1)*(-1)]/9=1/9=0.111111
.
.
.
Kompletną macierz wag przedstawia tabela:
|
|
Neuron 1 |
Neuron 2 |
Neuron 3 |
Neuron 4 |
Neuron 5 |
Neuron 6 |
Neuron 7 |
Neuron 8 |
Neuron 9 |
|
Neuron 1 |
0 |
0.111111 |
0.333333 |
0.111111 |
0.111111 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
|
Neuron 2 |
0.111111 |
0 |
0.111111 |
0.333333 |
-0.111111 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
|
Neuron 3 |
0.333333 |
0.111111 |
0 |
0.111111 |
0.111111 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
|
Neuron 4 |
0.111111 |
0.333333 |
0.111111 |
0 |
-0.111111 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
|
Neuron 5 |
0.111111 |
-0.111111 |
0.111111 |
-0.111111 |
0 |
-0.111111 |
0.111111 |
-0.111111 |
0.111111 |
|
Neuron 6 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
-0.111111 |
0 |
0.111111 |
0.333333 |
0.111111 |
|
Neuron 7 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
0.111111 |
0.111111 |
0 |
0.111111 |
0.333333 |
|
Neuron 8 |
0.111111 |
0.333333 |
0.111111 |
0.333333 |
-0.111111 |
0.333333 |
0.111111 |
0 |
0.111111 |
|
Neuron 9 |
0.333333 |
0.111111 |
0.333333 |
0.111111 |
0.111111 |
0.111111 |
0.333333 |
0.111111 |
0 |
Na rysunku zawartym w symulacji pokazano wartości wejściowe wektora testowego (w kolejnym kroku, po przepisaniu na wyjścia neuronów są one zerowane), wyjścia sumatora wag, wartości wyjściowe, oraz wartości wyjściowe z poprzedniego kroku obliczeń (wartości kwadratów umieszczonych w kolumnie).
Okazuje się, że gdy na wejście sieci podamy wektor identyczny z wzorcem, wówczas sieć nie zmieni swojego stanu, rozpoznaje ona również obrazy „niewiele” różniące się od wzorców. W niektórych przypadkach pojawia się kolejna cecha sieci Hopfielda - pamiętanie zależności pomiędzy sąsiednimi pikselami, a nie ich wartości. Wtedy otrzymujemy obraz wzorca z odwróconymi kolorami.
Wykonali:
Opiekun: mgr inż. A.Gołda
Czerwiec 2005