Introduction to neural networks


     ::History::

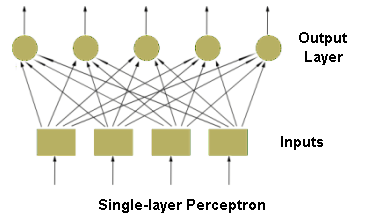
     The artificial intelligence has its origins in the fortieths of the twentieth century. Perceptron In 1943 McCulloch and Pitts elaborated model of human and animal neuron and explained the principles of combination of neurons i.e. neural network. Further advancement in this field of science contributed to introduction and design of perceptron (Rosenblatt, 1958). Its task was to recognise alphanumeric signs. There were also attempts to use neural networks among other things to weather forecast, identification of mathematical formulas, or analysis of electrocardiogram.

     In 1969 Minski and Papert published the monograph in which they proved that one-layer perceptron-like nets has limited area of application. This fact discouraged scientists from working on perceptrons and moved theirs interests towards expert systems. In the middle of the eighties some papers which proved that multi-layer non-linear neural networks has not limitations appeared. It caused growth of interests of this field of knowledge. The technology development of VLSI integrated circuits contributed to improvement of neuro-computers in the same period of time. The very important achievements are different training methods of multi-layer neural networks, e.g. back-propagation algorithm.

Neuron      ::Neural network::

     The human brain which consists of 1010 cells is the archetype of neural networks. There is about 1015 connections (synapses) between the cells. The neuron works with the frequency from 1 to 100 Hz. Consequently the approximated rate equals about 1018 operations per second and is many times greater than features of nowadays computers. Neural network is a simple model of brain. It consists of great number of neurons i.e. elements that process information. Neurons are formed in specified manners (see 'Neural Networks').

     ::Neuron model::

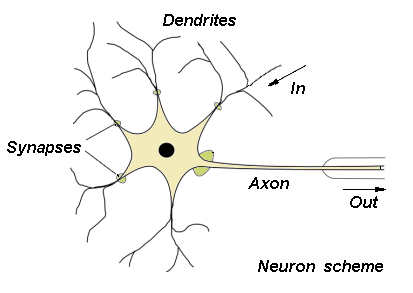
     The scheme of the neuron can be made on the basis of the biological cell. Such element consists of several inputs. The input signals are multiplied by the appropriate weights and then summed. The result is recalculated by an activation function.

    

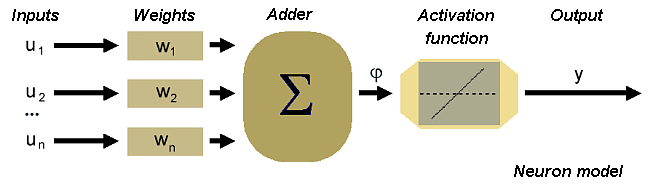
Neuron sztuczny


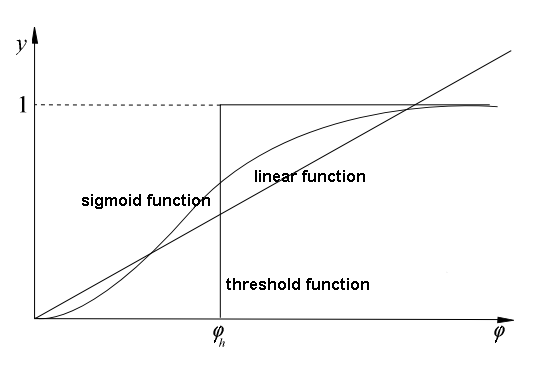
     In accordance with such model, the formula of the activation potential φ is as follows

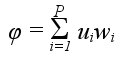
formula 1

     Signal φ is processed by activation function, which can take different shapes. If the function is linear the output signal can be described as:

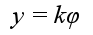
formula 2

Neural networks described by above formula are called linear neural networks.
The other type of activation function is threshold function:
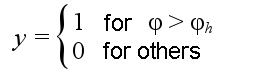
formula 3

where φh is a given constant threshold value.
Functions that more accurate describe the non-linear characteristic of the biological neuron activation function are:
sigmoid function:
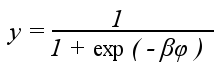
formula 4

where β is a parameter,
and hyperbolic tangent function:
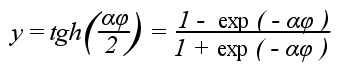
formula 5

where α is a parameter.

The next picture presents the graphs of particular activation functions:
  1. linear function,
  2. threshold function,
  3. sigmoid function.
chart

     ::Neural networks::

     There are different types of neural networks, which can be distinguished on the basis of their structure and directions of signal flow. Each kind of neural network has its own method of training. Generally, neural networks may be differentiated as follows

  • feedforward networks
    • one-layer networks
    • multi-layer networks
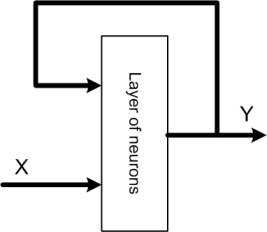
  • recurrent networks
  • cellular networks
Feedforward neural networks, which typical example is one-layer perceptron (see figure of Single-layer perceptron), consist of neurons set in layers. The information flow has one direction. Neurons from a layer are connected only with the neurons from the preceding layer. The multi-layer networks usually consist of input, hidden (one or more), and output layers. Such system may be treated as non-linear function approximation block: y = f(u).

Recurrent neural networks. Such networks have feedback loops (at least one) – output signals of a layer are connected to its inputs. It causes dynamic effects during network work. Input signals of layer consist of input and output states (from the previous step) of that layer. The structure of recurrent network depicts the below figure.

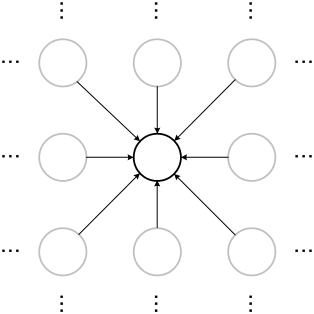
recurrent network


Cellular networks. In this type of neural networks neurons are arranged in a lattice. The connections (usually non-linear) may appear between the closest neurons. The typical example of such networks is Kohonen Self-Organising-Map.

recurrent network


References
Ryszard Tadeusiewcz "Sieci neuronowe", Kraków 1992
Józef Korbicz, Andrzej Obuchowicz, Dariusz Uciński "Sztuczne sieci neuronowe. Podstawy i zastosowania", Warszawa 1994
Simon Haykin "Neural Networks. A Comprehensive Foundation", New Jersey 1999
Andrzej Kos, (Lecture) "Przemysłowe zastosowania sztucznej inteligencji", 2003/2004
(WWW) Wstęp do sieci neuronowych

MSc. Adam Gołda
AGH-UST, 2005