Teoria problemu XOR

Neurony ułożone w jednej warstwie tak, że każdy z nich posiada polaryzację (waga b₁ prowadząca od sygnału jednostkowego) i wagi W_ij (które prowadzą od wejść x_j), tworzą tzw. sieć jednowarstwową. Parametry powyższe ustalają się podczas procesu uczenia się sieci (sygnały wyjściowe y_i dopasowują się do sygnałów zadanych u_i) (Rys. 1). Sieć taka ma ograniczone możliwości. Przykładem tego jest realizacja funkcji logicznej XOR (W opisie założono funkcję aktywacji – skok jednostkowy).

Rys. 1. Sieć jednowarstwowa

O możliwości uczenia się sieci neuronowej decyduje tzw. separowalność liniowa danych uczących (jedna prosta separuje zbiór danych, które odpowiadają u=1, od zbioru danych, które odpowiadają u=0).Warunki takie spelniaja np. funckje OR i AND.

Dla przykładu, funkcja AND posiada następujący zbiór wektorów uczących (Tabela 1)

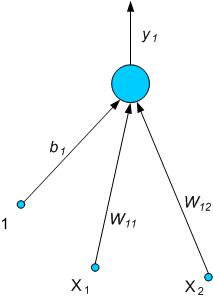
Tabela 1. Zbiór wektorów uczących funkcji AND

Sieć neuronowa, która taką funkcję realizuje, złożona jest z jednego neuronu wyjściowego o dwóch wejściach x₁, x₂ oraz polaryzacji b₁ (Rys. 2).

Rys. 2. Sieć neuronowa realizująca funkcję AND

Podczas uczenia się sieci, należy przyjąć, że y₁ = f ( W₁₁x₁ + W₁₂x₂ + b₁ ) = u₁, co przedstawione zostało na Rysunku 3.

Rys. 3. Separowalność liniowa w przypadku funkcji AND

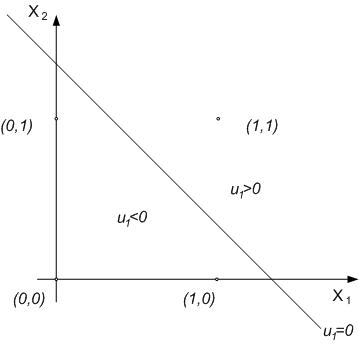
Jak wynika z Tabeli 1, na wyjściu powinniśmy otrzymać '1' tylko w punkcie (1,1). Prosta, która realizuje w tym przypadku separowalność liniową, ma równanie u₁ = W₁₁x₁ + W₁₂x₂ + b₁. Zatem, poprzez dobranie jej współczynników (W₁₁, W₁₂ i b₁), możemy ją tak wyznaczyć, by tą separowalność uzyskać. Jak widać na Rysunku 3, dla funkcji AND nie stanowi to dużego problemu.



Separowalności liniowej nie wykazuje układ realizujący funkcję XOR (której zbiór wektorów uczących przedstawia Tabela 2).

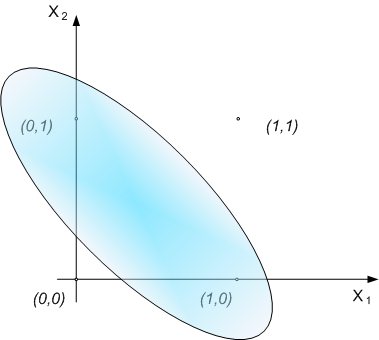
Tabela 2. Zbiór wektorów uczących funkcji XOR

Oznacza to, że nie da się wyznaczyć linii oddzielającej przestrzeń danych na 2 mniejsze, z których jedna odpowiada sygnałowi 1 na wyjściu, a druga 0 na wyjściu (Rys. 4). Wnętrze owalnego obszaru odpowiada 1 na wyjściu, zewnętrze – 0. Nie da się tego zrealizować, stosując podział za pomocą jednej prostej.

Rys. 4. Przestrzeń danych funkcji XOR

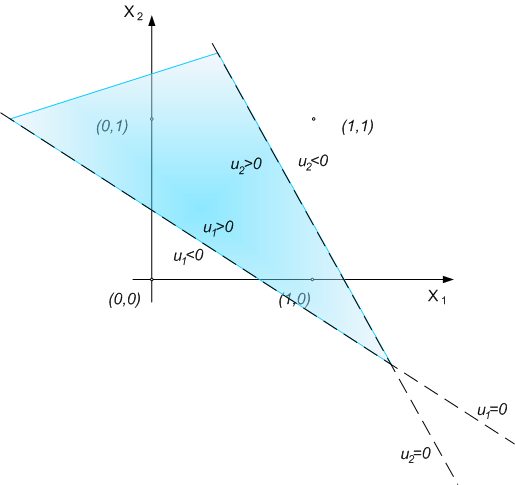
Nie mają tu znaczenia współczynniki tej prostej, czyli wagi W₁₁, W₁₂, b₁. Nie można zatem za pomocą jednego perceptronu zrealizować funkcji logicznej XOR.

Rozwiązaniem tego problemu jest rozszerzenie sieci neuronowej w taki sposób, by dodając jeden neuron w warstwie stworzyć sieć neuronów o wagach realizujących następujący podział przestrzeni:

1) dla 1-ego neuronu

u₁ = W₁₁x₁ + W₁₂x ₂ + b₁ > 0
u₁ = W₂₁x₁ + W₂₂x ₂ + b₁ < 0

2) dla 2-ego neuronu

u₂ = W₂₁x₁ + W₂₂x ₂ + b₂ > 0
u₂ = W₂₁x₁ + W₂₂x ₂ + b₂ < 0

Podział powinien być taki, jak na rysunku 5.

Rys. 5. Sposób realizacji funkcji XOR za pomocą sieci wielowarstwowej

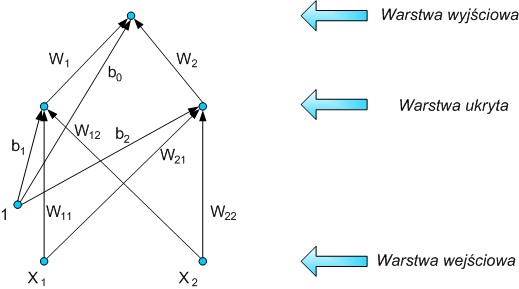
Po dodaniu dodatkowej warstwy z neuronem, możliwe staje się zrealizowanie sumy logicznej, która na wykresie przedstawia się jako część wspólna zbiorów u₁>0 i u₂>0. Na rysunku 6 można zobaczyć pełną strukturę sieci neuronowej mogącej realizować funkcję XOR. Każdy dodatkowy neuron umożliwia dokonanie liniowego podziału na granicy u_i>0 i u_i<0 zależnej od wag neuronu. Warstwą wyjściową jest tu taki obszar, który jest kombinacją obszarów mniejszych powstałych z podziału obszaru danych wejściowych (przez dodatkowy neuron).

Rys. 6. Struktura sieci mogącej realizować funkcję XOR