A clause is defined as a sum (logical OR) of Literals.
A Literal is either:
- an atomic formula (denoted as
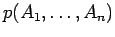 ), or
), or
- a negated atomic formula (denoted as
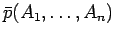 or
or
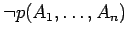 ).
).
A negated atomic formula is a Negative Literal.
A not negated formula is a Positive Literal.
A Horn Clause is a clause with at most one positive literal, it is thus either:
- A single positive literal, which is regarded as a fact,
- One or more negative literals, with no positive literal, or
- A positive literal and one or more negative literals which is a rule.
A subset of Horn Clauses, generated by groups 1 and 3, expresses knowledge in Datalog.
Horn Clauses of group 3 are considered rules [22].
The following Horn Clause:
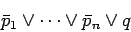 |
(4.1) |
is logically equivalent to:
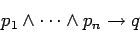 |
(4.2) |
where 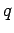 is called the head of the rule, and
is called the head of the rule, and
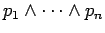 is called the body.
Each of the
is called the body.
Each of the 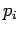 is called a subgoal;
is called a subgoal;
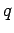 can also be called the conclusion, and
can also be called the conclusion, and 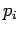 can be called the preconditions.
can be called the preconditions.
Igor Wojnicki
2005-11-07