Next: Solvable problems Up: Solution Analysis and Properties Previous: Solution Analysis and Properties Contents
A relational database can be represented as a logic program which consists of bare facts (see Chapters 4 and 6). The relational model and the logic program (expressed by Datalog or Prolog), are isomorphic unless the names of the columns in the tables are considered [17].
From the mathematical point of view, there is no difference between these two representations. When the mathematical basis of the relational model is extended with attributes, then a difference appears. In the extended relational model a value is referred by the attribute name, or its position in the relation schema9.1. For the logic program, a predicate has no attribute. The only way a value may be referred to, is its position (see Section 4).
The basic operations of relational algebra which are: union, set difference, Cartesian product, projection, and selection (see Section 3.2), may be expressed with logic programs. So Logic programs have at least the computational power of relational algebra [17].
The Union of relations ![]() and
and ![]() which is denoted as:
which is denoted as: ![]() (see Section 3.2, Definition 3.2) can be expressed by two rules (regarding rules see Chapter 4), assuming that predicates
(see Section 3.2, Definition 3.2) can be expressed by two rules (regarding rules see Chapter 4), assuming that predicates ![]() and
and ![]() denote relations
denote relations ![]() and
and ![]() respectively:
respectively:
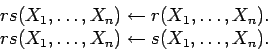 |
(9.1) |
The difference of two relations ![]() and
and ![]() which is denoted as:
which is denoted as: ![]() (see Section 3.2, Definition 3.3) is expressed using a negation (
(see Section 3.2, Definition 3.3) is expressed using a negation (![]() ) (for the meaning of
) (for the meaning of ![]() in Prolog refer to Section 6.1).
Assuming that
in Prolog refer to Section 6.1).
Assuming that ![]() is a predicate representing the resulting relation, and
is a predicate representing the resulting relation, and ![]() ,
, ![]() are predicates representing relations:
are predicates representing relations: ![]() and
and ![]() respectively, the difference can be expressed as follows:
respectively, the difference can be expressed as follows:
| (9.2) |
The Cartesian product of two relations ![]() and
and ![]() , denoted as
, denoted as ![]() (see Section 3.2, Definition 3.4) is represented by the following rule:
(see Section 3.2, Definition 3.4) is represented by the following rule:
| (9.3) |
The projection and selection can be expressed as well.
Assuming that there is a relation schema ![]() , and
, and ![]() is an ordered set of attributes:
is an ordered set of attributes:
![]() .
The projection is denoted as:
.
The projection is denoted as:
| (9.4) |
The selection is denoted as:
| (9.5) |
All other relational algebra operations can be expressed with these basic ones, so logical programs can be used to express any relational algebra operation.
There is another issue which has to be pointed out. The domains for relations are explicitly stated in the relational model. If the elements are not enumerated, at least their types are stated as integers, characters etc. Prolog does not have such a typing system. Originally, it does not provide any restrictions to what a term is9.2. While the terms are being instantiated, certain values become valid for them. So there is a single domain of terms.
Igor Wojnicki 2005-11-07