Temat 25: Dynamika ciała sztywnego w ruchu postępowym i obrotowym

 

24.1. Równania dynamiczne ciała sztywnego w ruchu postępowym

 
    Załóżmy, że mamy ciało obciążone siłami zewnętrznymi ... , , które porusza się ruchem postępowym. Zatem, aby wyznaczyć zależność między przyspieszeniem  ciała, a siłami zewnętrznymi działającymi na to ciało (rys. 24.1), skorzystamy z twierdzenia o ruchu środka masy.
Równanie wynikające z tego twierdzenia w rozpatrywanym przypadku ma następującą postać:

,                                                                                                                  (24.1)                        

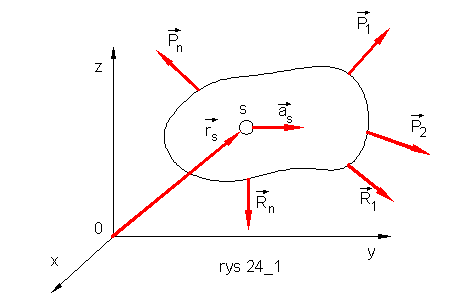
 gdzie:
 M     - masa ciała,
 - suma geometryczna sił czynnych i reakcji lub po zrzutowaniu obu stron równania (24.1) na osie Ox, Oy, Oz ma  postać:

, 

,                                                                                                                                               (24.2)                    

.          

 

Ustalimy dodatkowo, w jaki sposób siły zewnętrzne muszą być przyłożone do ciała sztywnego, aby mógł zachodzić ruch postępowy, korzystając z twierdzenia pochodnej krętu wyznaczonego względem środka masy ciała:

                                                                                                        (24.3)


    Każde ciało materialne można traktować jako graniczny przypadek układu punktów materialnych, zatem twierdzenie to można zastosować do rozpatrywanego tu ciała sztywnego. Z uwagi na to, że w ruchu postępowym wszystkie punkty ciała mają prędkość taką samą jak środek tego ciała, przeto: , gdyż prędkości punktów ciała względem środka masy S są równe zeru.  

Z równania (24.3) wynika teraz, że gdy ciało porusza się ruchem postępowym, wówczas

.                                                                                                                                                                (24.4)
 Otrzymaliśmy więc następujący warunek:

Aby ciało sztywne mogło się poruszać ruchem postępowym, suma geometryczna momentów względem środka masy sił zewnętrznych działających na to ciało nie musi być równa zeru.


Przykład 1.
    Skip wielkiego pieca o ciężarze G = 3,27- 104 N opuszcza się po płaszczyźnie nachylonej do posuwu pod kątem a = 60° (rys. 24.2).
Dane: s = 3 ln (1 – to+t ), gdzie s w metrach, t w sekundach, t0  - chwila początkowa ruchu skipu, oraz współczynnik tarcia
 µ = 0,1. Obliczyć siłę w linie podczas opuszczania skipu.

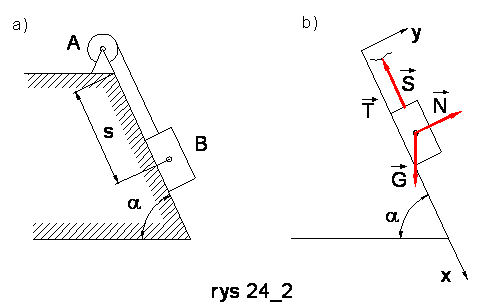
 Rozwiązanie:
    Ruch skipu odbywa się wskutek działania siły ciężkości. Rozpatrzymy ruch tylko samego skipu; w tym celu należy dokonać oswobodzenia ciała od więzów. W pomyślanym przecięciu liny przyłożymy siłę S. Równanie ruchu napiszemy w postaci:

,

 ,
 

,

          .
Wielkości x i y znajdujemy z równań ruchu

,         ,

,

.

Wstawiając do równania ruchu wyrażenia określające x i  y, otrzymujemy:

                ,

                ,

            ,

            ,

            ,

 
stąd

,

.

 

24.2. Równanie dynamiczne ruchu ciała sztywnego w ruchu obrotowym

    Rozpatrzymy ciało sztywne obracające się dookoła nieruchomej osi obrotu z prędkością kątową (rys. 24.3), pod działaniem sił zewnętrznych . Kręt punktu Mi względem osi Oz jest równy:

           

 ,                                                                                                                                   (24.5)                      

 

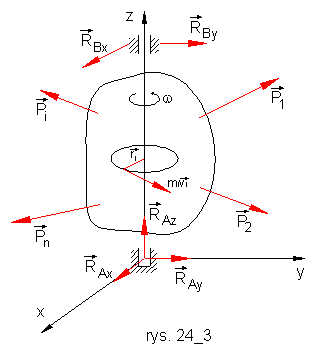
gdzie ri   jest   promieniem okręgu opisanego punktem Mi , vi = riω -  wartością prędkości punktu Mi.

Kret ciała sztywnego względem osi Oz wynosi:

 ,                                                                                                                         (24.6)

 
gdzie  jest  momentem  bezwładności   ciała względem osi Oz.

Korzystając z zasady krętu dla układu punktów materialnych

                                                                                                                                        (24.7)                             

oraz podstawiając w (24.7) równanie (24.6), otrzymujemy równanie dynamiczne ruchu obrotowego dla ciała sztywnego:

            .                                                                                                                                            (24.8)

 

Jeżeli > 0 to ε =  - ciało porusza się ruchem przyspieszonym.

Jeżeli = 0 to ε =  - ciało porusza się ruchem jednostajnym.

Jeżeli < 0 to ε =  - ciało porusza się ruchem opóźnionym.

 


Przykład 2.
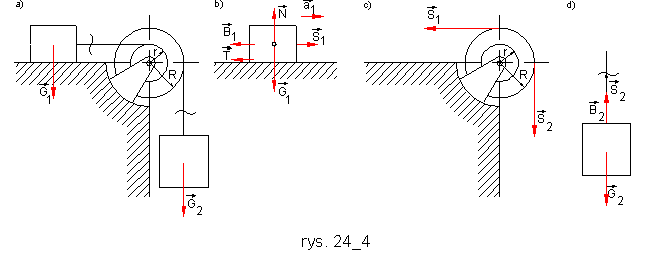
    Dla układu przedstawionego na rysunku 24.4a obliczyć przyspieszenie kątowe ε krążka, jeżeli:

G1=500 N,       G2 = 4000N,       J = 100 kgm2,        R = 0,2 m,        r = 0,1 m,        µ = 0,4 


Rozwiązanie:

    Układ nasz składa się z trzech brył. Rozpatrywać będziemy ruch każdej bryły z osobna uwzględniając wzajemne oddziaływanie brył na siebie. Rozpatrujemy ruch bryły o ciężarze  (rys. 24.4b). Na bryłę o ciężarze  działają następujące siły: siła naciągu w sznurze , siła tarcia  oraz siła reakcji normalnej .

 

Równanie ruchu napiszemy na podstawie zasady d'Alemberta. Do bryły przykła­damy pozorną siłę bezwładności  skierowaną przeciwnie do zwrotu przyspieszenia

.

 Wartość siły tarcia:

              .

 Wartość pozornej siły bezwładności:

            .

 Równanie ruchu przybierze więc postać:

            .

Następnie rozpatrzymy ruch krążka (rys. 24.4c). Krążek porusza; się ruchem obrotowym.

Równanie dynamiczne ruchu obrotowego ma postać:

          .

 Suma momentów wszystkich sił względem osi obrotu jest równa:

            ,

stąd:

            ,

Rozpatrzymy teraz ruch ciała o ciężarze  (rys. 24.4d). Równanie ruchu tego ciała napiszemy także na podstawie zasady d'Alemberta. W tym celu przyłożymy do ciała o ciężarze  pozorną siłę bezwładności . Równanie ruchu ma więc postać:

,

,

stąd:

            .

 Otrzymaliśmy tym sposobem trzy równania:

,

,

.

Między przyspieszeniem kątowym a przyspieszeniem ciała o ciężarze  zachodzi związek:

,

 a między ε a przyspieszeniem ciała o ciężarze

.

 Uwzględniając dwa ostatnie wyrażenia po przekształceniach, otrzymujemy:

 

            .

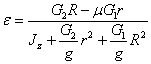Po podstawieniu danych otrzymamy:

 

.

 

24.3. Wahadło fizyczne

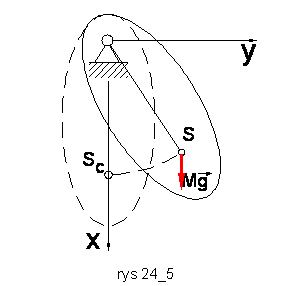
    Ciało materialne, które może się swobodnie obracać dookoła poziomej osi, nosi nazwę wahadła fizycznego (rys. 24.5). Obierzmy układ współrzędnych Oxyz tak, aby oś Oz pokrywała się z osią obrotu wahadła, a pozostałe dwie osie były skierowane w sposób podany na rysunku. Położenie ciała w dowolnej chwili t możnat określić za pomocą kąta φ, który prosta OS tworzy z osią x. Położenie równowagi stałej wahadła odpo­wiada wartości kąta φ = 0. Pomijając tarcie w łożysku osi obrotu wahadła i opór powietrza, otrzymujemy, że jedyną siłą dającą moment względem osi obrotu wahadła Oz jest siła ciężkości . Oznaczając odległość środka masy wahadła do osi obrotu  b=OS otrzymujemy:

 

.   Równanie (24.8) ma wówczas postać:

 

                                                                                                                                                                    (24.9)

 

 albo

                .                                                                                                                                                               (24.10)                                Porównując otrzymane równanie z równaniem ruchu wahadła matematycznego widzimy, że mają one taką samą postać.

Oznaczając symbolem lr ,otrzymujemy:

 

,                                                                                                                                                                  (24.11)

 

gdzie lr jest długością zredukowaną wahadła fizycznego. Długość zredukowana lr jest to taka długość, przy której wahadło matematyczne ma, ten sam okres, co wahadło fizyczne.

Ponieważ zgodnie z twierdzeniem Steinera ,  więc długość lr można napisać w postaci:

 

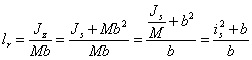            ,                                                                                                    (24.12)

 

gdzie is jest ramieniem bezwładności wahadła względem osi przechodzącej przez środek masy.

Otrzymana zależność (24.11) służy do wyznaczania momentów bezwładności brył. Z pomiaru T możemy wyliczyć lr a następnie przy znanym b obliczymy is.



Pytania i ćwiczenia sprawdzające


  1. Podać równania dynamiczne ciała sztywnego w ruchu postępowym.

2. Podać równania dynamiczne ciała sztywnego w ruchu obrotowym.

3. Co to jest wahadło fizyczne?

4. Co to jest długość zredukowana wahadła fizycznego?

 Ćwiczenia

   
Wyprowadź zależność służącą do wyznaczania przyśpieszenia grawitacyjnego posługując się wahadłem matematycznym (szczególny przypadek wahadła fizycznego).

Odpowiedź: