Temat 26:    Dynamika ciała sztywnego w ruchu płaskim


     
     Na rysunku 26.1 przedstawiono przekrój ciała sztywnego poruszającego się ruchem płaskim w płaszczyźnie kierowniczej, przechodzącej przez środek masy S.


     Przedsta­wiony na rysunku układ osi współrzędnych Oxyz jest układem nieruchomym, na­tomiast układu 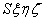porusza się ruchem postępowym z prędkością środka masy .  W celu otrzymania równań dynamicznych ruchu płaskiego oprzemy się na twierdzeniu o ruchu środka masy oraz na zasadzie krętu układu materialnego w ruchu względem środka masy.
Otrzymujemy stąd dwa następujące równania wektorowe:  
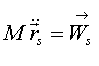                                                                                                                                                                                        (26.1)                            
   
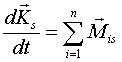
gdzie:
     M -  masa ciała,
     rs  -  promień-wektor środka masy S,  
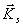    - kręt ciała względem środka masy,
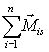     - suma momentów sił zewnętrznych względem tego środka.
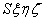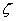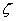Ruch rozpatrywanego ciała sztywnego względem środka masy, czyli ściślej względem układu jest ruchem obrotowym, a osią obrotu jest oś S , nie zmieniająca swego położenia względem badanego ciała. Wzdłuż tej osi skierowany jest wektor pręd­kości kątowej . Składową krętu K wzdłuż osi  S 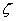możemy otrzymać bezpośrednio ze wzoru (12.6): 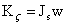, przy czym Js jest momentem bezwładności względem osi S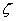 , przechodzącej przez środek masy. Oznaczając kąt obrotu  φ  mierzony tak, jak na rysunku 26.1, otrzymujemy:   = φ'. Biorąc pod uwagę powyższe zależ­ności, z równań (12.16), otrzymu­jemy trzy następujące równania, dy­namiczne ruchu płaskiego:

   
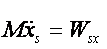
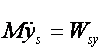                                                                                                                                                                                      (26.2)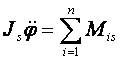
   
gdzie xs, ys są współrzędnymi środka masy S w układzie współrzędnych Oxyz  a 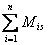  -   momentem sił. względem osi S .

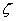Przykład 1.
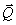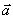Walec o ciężarze i  promieniu r owinięty jest nicią, której koniec zamocowany jest do sufitu, tak jak pokazano na (rys. 26.2). Znaleźć przyspieszenie środka walca podczas jego ruchu w dół. Obliczyć również przyspieszenie kątowe e oraz siłę 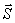w nici (rys. 26.2).

Rozwiązanie:
Równania dynamiczne w ruchu płaskim mają postać:
   
   
   
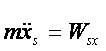
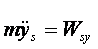
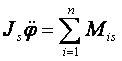
W naszym przypadku środek masy walca porusza się po lini prostej wzdłuż osi y.
Odpadnie więc równanie pierwsze.  
Równanie drugie ma postać:

   
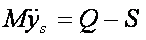
Równanie trzecie:
   
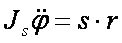
Moment bezwładności:
   

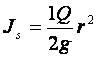
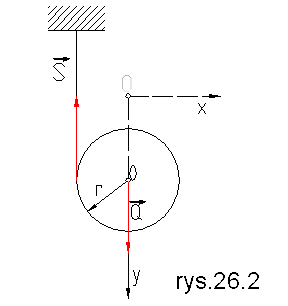
Uwzględniając ostatnie wyrażenie możemy napisac:
   
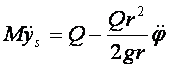
Ponieważ:
   
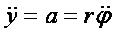
wiec:
   
Przyspieszenie kątowe:

.......................................
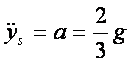
Siła 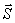naciągu nici: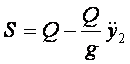
   
Czyli:
   

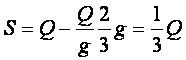
Przykład 2.
Walec o promieniu r i ciężarze 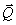stacza się bez poślizgu po równi pochyłej o kącie nachylenia 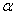(rys. 26.3) . Znaleźć przyspieszenie środka walca. 

Rozwiązanie:

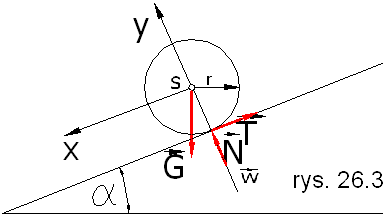
Jeżeli zachodzi toczenie się walca bez poślizgu, to punkt C jest chwilowym środkiem obrotu, walec bowiem porusza się ruchem płaskim. Równanie dynamiczne ruchu walca ma postać:
   
   
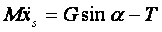
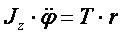
stąd
   
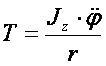
Wiadomo ,że
   
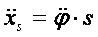
stąd
   
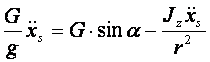
Moment bezwładności walca względem jego osi jest równy:
   
   
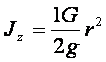
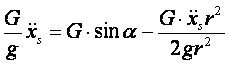
Po przekształceniach otrzymujemy:
   

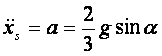
Pytania i ćwiczenia sprawdzające:

       1. Podać na jakim twierdzeniu i jakiej zasadzie opieramy się wyprowadzając równania dynamiczne ciała sztywnego w  ruchu płaskim?
       2. Podać  równania dynamiczne ciała sztywnego w ruchu płaskim.

Ćwiczenia:

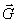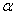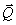1.  Ciężar zsuwa się po płaskiej równi pochyłej tworzącej kąt . Ciało to za pośrednictwem nieważkiej i nierozciągliwej nici wprawia w ruch bęben o ciężarze i promieniu r (rys. 26.4). Obliczyć przyspieszenie kątowe bębna, który jest walcem kołowym. Masę nieruchomego krążka można pominąć.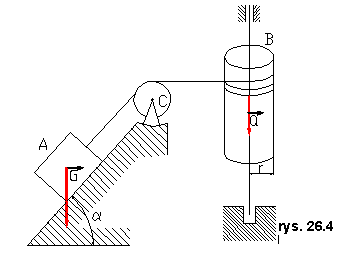

Odpowiedź:

   

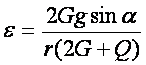
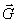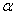2. Na bęben o promieniu b jednorodnego walca o ciężarze i promieniu r, leżącego na płaszczyźnie poziomej, nawinięta jest nić, którą ciągnie siła P, tworząca z poziomem kąt . Ramię bezwładności walca wynosi ρ (rys 26.5). Wyprowadzić równanie ruchu osi bębna.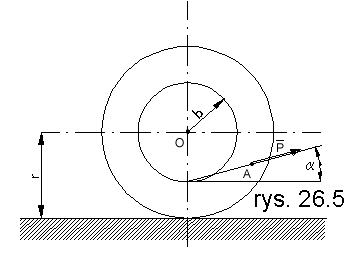


Odpowiedź: