AGH
Wydział Inżynierii Materiałowej i Ceramiki AGH
Studia I stopnia Chemia Budowlana rok II – Plan zajęć
Temat ćwiczenia laboratoryjnego:
Analiza przetwarzania analogowo-cyfrowego
z zastosowaniem pakietu
Matlab
Warunek dopuszczenia do ćwiczenia:
a) Opanowanie wiadomości teoretycznych dotyczących przetworników analogowo-cyfrowych, na podstawie wykładu, podręczników oraz kompendium zamieszczonego TUTAJ
b) Umiejętność odpowiedzi na pytania dotyczące: próbkowania, kwantowania, kodowania, twierdzenia o próbkowaniu, zjawiska aliasingu, oraz celu przetwarzania A/C i podstawowych typów przetworników A/C
Cele ćwiczenia:
- Poznanie przeznaczenia i podstaw użytkowania pakietu matematycznego Matlab oraz sposobów wykonywania w nim prostych obliczeń z zastosowaniem funkcji trygonometrycznych.
- Poznanie podstawowych sposobów generowania wykresów i pisania programów w Matlabie.
- Poznanie elementów budowy graficznych programów dialogowych w Matlabie (z użyciem t.zw.: GUI - Graphic User Interface).
- Obserwowanie procesu dyskretyzacji sygnału przez próbkowanie - przy pomocy aplikacji graficznej w Matlabie
- Obserwacja zjawiska alisingu i doświadczalne sprawdzanie twierdzenia o próbkowaniu z zastosowaniem funkcji FFT (szybkiej transformaty Fourier'a).
Literatura:
Wacław Gawędzki:
Pomiary Elektryczne (podręcznik pdf)
Roman Kaula:
Wprowadzenie - Środowisko obliczeń numerycznych Matlab-Simulink (pdf)
https://www.mathworks.com/matlabcentral/fileexchange/27105-wprowadzenie-do-matlaba--introduction-to-matlab-in-polish-
Instrukcja do ćwiczenia:
1. Środowisko MATLABa i praca w Oknie Komend oraz korzystanie z HELP
|
W takich ramkach z zielonym tłem umieszczane będą OBJAŚNIENIA.
MATLAB (którego nazwa pochodzi od MATrix LABoratory - laboratorium macierzowe)
- to pakiet oprogramowania matematycznego firmy MathWorks Inc. rozwijany od roku 1984.
Zawiera on:
- język i środowisko programowania do obliczeń naukowo-technicznych
oraz
- bardzo bogaty zestaw wyspecjalizowanych tematycznych bibliotek podprogramów (toolbox’ów)
- i wiele tysięcy stron (na CD) podręczników, przykładów i aplikacji demonstracyjnych (demos)
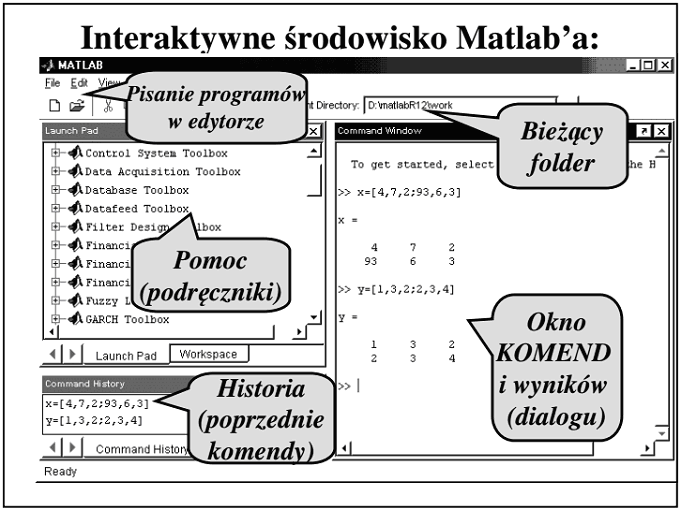
Interaktywne środowisko programowania Matlaba
(t.zw. IDE - od ang.:Interactive Development Environment)
może
składać się z wielu okien.
Najważniejsze - OKNO KOMEND (ang.: Command Window) - służy do wpisywania poleceń w języku Matlaba i w tym samym oknie wyświetlane są wyniki, objaśnienia i komunikaty o błędach.
Działając tylko w OKNIE KOMEND można pozamykać inne okna a przywrócić można je z menu: Desktop - Desktop_Layout - Default.
Objaśnienia można wyszukiwać z menu głównego HELP.
Drugi sposób to wpisanie słowa "help", a po nim nazwy funkcji lub określenia grupy funkcji czy innych elementów Matlaba np.:
help lang - pomoc dotycząca elementów języka,
help ops - pomoc dotycząca operatorów,
help elfun - pomoc dotycząca funkcji elementarnych,
help iofun - pomoc dotycząca funkcji wejścia-wyjścia.
Klawisz "strzałka w górę" przywołuje poprzednio wpisane polecenia i można je wykonywać ponownie a także zmieniać.
Okno komend można wyczyścić komendą clc.
|
Zad.1: Korzystanie z HELP. Czyszczenie Okna Komend
a) Znajdź (jak wyżej) objaśnienia dotyczące operatorów Matlaba, następnie wyczyść okno komendą clc
b) Znajdź objaśnienia funkcji pierwiastek kwadratowy (ang.: square root) z grupy funkcji elementarnych (help elfun) i znów wyczyść okno komend.
2. Stałe liczbowe i operatory działań. Obliczanie wartości wyrażeń arytmetycznych
Objaśnienia:
Pojedyncze linie poleceń można wpisywać w oknie komend gdy jest tam znak gotowości: [>>]. Linię kończy naciśnięcie ENTER.
W jednej linii można wpisać jedno lub kilka poleceń i wtedy oddzielamy je przecinkami lub średnikami.
Średnik [;] na końcu polecenia zapobiega wyświetleniu wyniku działania tego polecenia.
Najprostszym poleceniem jest
WYRAŻENIE arytmetyczne.
Matlab wyznaczy jego wartość i wyświetli (jeśli po wyrażeniu nie umieścimy średnika).
Wyrażeniem jest także pojedyncza zmienna lub wywołanie funkcji.
Wpisując liczby pamiętajmy, że separatorem części ułamkowej jest KROPKA a nie przecinek.
Operacje arytmetyczne (dotyczące skalarów) wykonywane są w następującej kolejności:
- wyznaczanie wartości funkcji i wyrażeń w nawiasach ( )
- potęgowanie (^)
- zmiana znaku (–)
- mnożenie i dzielenie (* /)
- dodawanie i odejmowanie (+ –)
Pomoc dotyczącą operatorów uzyskasz wpisując: help ops
więcej objaśnień masz m.in. TUTAJ
|
Nazwy funkcji Matlaba pisane są małymi literami a po nazwie zawsze występują nawiasy okrągłe obejmujące argumenty funkcji. Oto niektóre funkcje operujące na skalarach lub elementach wektorów i macierzy:
- sqrt(x) - pierwiastek kwadratowy z x
- sin(x), cos(x), tan(x) - funkcje trygonometryczne
- abs(x) - wartość bezwzględna
- exp(x) - funkcja wykładnicza ex
- log(x) - logarytm naturalny
- log10(x) - logarytm dziesiętny
- round(x) - zaokrąglenie do najbliższej całkowitej
|
|
Zad.2: Obliczanie wartości funkcji i wyrażeń:
- Sprawdź wyniki kilku prostych działań np.: 2x2 2,5x2 pierwiastek z 9 (Uwaga: stosuj znaki Matlaba!)
- Sprawdz czy Matlab zna stałą pi (tak właśnie wpisaną)? Oblicz 2π. Pamiętaj: NIE WOLNO POMIJAĆ ZNAKU MNOŻENIA!
- Sprawdź czy sinus 30 stopni wynosi 0,5 (jak powinien!), jeśli nie to przeczytaj w "help sin" w jakich jednostkach ma być kąt i popraw wykorzystując stałą pi.
3. Zmienne i instrukcje przypisania
|
Zmienne służą do przechowywania wartości różnych typów. Do nadawania wartości zmiennym lub ich zmieniania służą instrukcje przypisania (zwane też instrukcjami podstawiania). W Matlabie nie trzeba deklarować typu zmiennej gdyż jest on samoczynnie (dynamicznie) określany na podstawie przypisanej wartości. Tej samej zmiennej można przypisać wartość liczbową np.:5 a za chwilę wartość tekstową np.: 'Ala'. Domyślnie wszystkie zmienne traktowane są jak macierze a jeśli mają rozmiar 1x1 to są skalarami. Wykaz aktualnie istniejących zmienne podają polecenia who i whos, a usuwa zmienne z pamięci polecenie clear.
Nazwy zmiennych można tworzyć z liter angielskich i cyfr (oraz znaku podkreślnika) ale pierwszym znakiem nazwy zmiennej musi być litera.
Uwaga: dotyczy to także nazw podprogramów i plików z programami.
Instrukcja przypisania ZMIENNEJ wartości WYRAŻENIA ma postać:
ZMIENNA = WYRAŻENIE
- rozkazuje ona komputerowi wyznaczyć wartość WYRAŻENIA i przesłać ją do obszaru pamięci przypisanego ZMIENNEJ.
Zauważ, że zawsze ZMIENNA zapisana jest po lewej stronie a WYRAŻENIE po prawej, nie odwrotnie!
Gdy nie wstawimy wyniku wyrażenia do żadnej zmiennej wówczas MATLAB tworzy zmienną „ans” (od angielskiego "answer" = odpowiedź).
Matlab rozróżnia małe i duże litery. Słowa kluczowe i nazwy funkcji Matlaba trzeba wpisywać małymi.
Dokładniejsze objaśnienia masz
TUTAJ
|
Zad.3: Obliczenia z użyciem zmiennych
Wpisz w oknie komend (po każdej linii ENTER) i wyciągnij wnioski:
w=sqrt(9);
w
w=w+1
-
Nadaj zmiennej x podaną niżej wartość, następnie wyznacz y w/g podanego wzoru,
potem wstaw do x drugą z podanych wartość i powtórz (używając klawisza strzałki) operację obliczania y
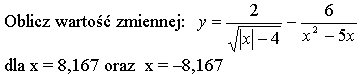
(Uwaga: klawisz "strzałka w górę" wywołuje poprzednio napisane komendy i nie trzeba ich wpisywać jeszcze raz.)
(Poprawne wartości y to: 0.7478 oraz 0.9240)
Wyświetl wykaz zmiennych, komendami who oraz whos, następnie wyczyść pamięć komendą clear i ponownie wpisz whos.
4. Wektory, macierze, ciągi. Mnożenie macierzowe [*] i tablicowe [.*]
Dowolny wektor wierszowy definiujemy wpisując jego elementy w nawiasie prostokątnym i oddzielając je od siebie przecinkami.
Macierz też możemy zdefiniować podając jej elementy w nawiasie prostokątnym i oddzielając elementy wiersza przecinkami a wiersze średnikami np.:
|
V=[2.5, 6, 12, 4.55]
macierz=[1,6,3; 8,2,5]
|
Jesli w definicji wektora zamiast przecinków zastosujemy średniki to powstanie wektor kolumnowy np.:
Do zdefiniowania ciągu typu "postęp arytmetyczny" służy wyrażenie z dwukropkami:
pierwszy_element : przyrost : ostatni_element
Na przykład:
>> z=1:0.2:1.5
z =
1.0000 1.2000 1.4000
|
Jak widać w rzeczywistości ostatni element może być mniejszy jeśli tak wynika z dodawania podanego przyrostu.
Każdy ciąg jest zarazem wektorem (tu: wierszowym), podobnie jak funkcja której argumentem jest wektor daje w wyniku wektor. jednak przy mnożeniu, dzieleniu i potęgowaniu macierzy i wektorów obowiązują szczególne zasady i musimy je znać
oto przykłady:
>> y=sin(z)
y =
0.8415 0.9320 0.9854
|
Działania na wektorach i macierzach
Dodawanie i odejmowanie wektorów i macierzy jest możliwe gdy mają one identyczne rozmiary.
Ale UWAGA: zwykłe operatory mnożenia (*), potęgowania(^), dzielenia(/) są traktowane jako operacje macierzowe, które trzeba znać, bo inaczej doprowadzą do błędów:
>> y+z
ans =
1.8415 2.1320 2.3854
|
>> z*sin(z)
??? Error using ==> mtimes
Inner matrix dimensions must agree.
|
>> z^2
??? Error using ==> mpower
Matrix must be square.
|
>> z*z
??? Error using ==> mtimes
Inner matrix dimensions must agree.
|
Mnożenie macierzowe (*) to mnożenie elementów wiersza pierwszej macierzy przez elementy kolumny macierzy drugiej i wyznaczaniu sum takich iloczynów.
Natomiast operatory z kropką (.*), (.^), (./) to t.zw. operacje tablicowe - na parach odpowiadających sobie elementów dwu wektorów lub macierzy o identycznych rozmiarach (jak przy dodawaniu):
>> z.*sin(z)
ans =
0.8415 1.1184 1.3796
|
>> z.^2
ans =
1.0000 1.4400 1.9600
|
>> z.*z
ans =
1.0000 1.4400 1.9600
|
|
Zad.4
a) Wpisz w oknie komend definicje wektorów umieszczone powyżej w białych polach.
b) Zdefiniuj ciąg liczb naturalnych od 1 do 5 a następnie ciąg kwadratów tych liczb. Jaki rodzaj potęgowania należy zastosować?
5. WYKRESY XY
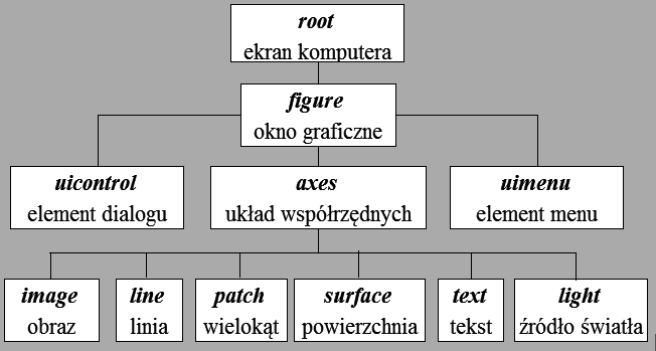
Matlab ma wiele funkcji do tworzenia wykresów. Do tworzenia wykresów typu XY (na płaszczyźnie) mogą służyć m.in.funkcje:
plot(x,y,'krz') - liniowy,
gdzie: 'krz' to max.3 znaki, określające kolor, rodzaj linii i znacznik,
bar(x,y) - słupkowy,
stem(x,y) - szpilkowy,
stairs(x,y) - schodkowy.
Podano tu najprostsze postaci tych funkcji gdyż mogą one mieć różną liczbę argumentów.
Argument x ma być wektorem (ciągiem) wartości dla osi X a argument y - wektorem wartości dla osi Y.
Wykres (obiekt typu line) powstaje w układzie współrzędnych zwanym axes a ten z kolei w oknie graficznym zwanym figure - tworzonym automatycznie lub przez użytkownika, poleceniem figure.
W oknie tym można też tworzyć aplikacje graficzne z innymi obiektami, a w szczególności elementami typu uicontrol (przyciskami, suwakami, ...) .
|
Zad.5:
a) Zdefiniuj ciąg wartości kąta x od zera co 3 stopnie aż do 360 stopni
b) Zdefiniuj wektor y=sin(x) i wykonaj wykres przy pomocy funkcji plot(x,y).
Czy wykres jest prawidłowy? Zapomnieliśmy o radianach? Spróbuj poprawić lub przejdź dalej gdzie zajęto się tym problemem.
6. Pisanie programów w edytorze. Programy rysujące wykresy
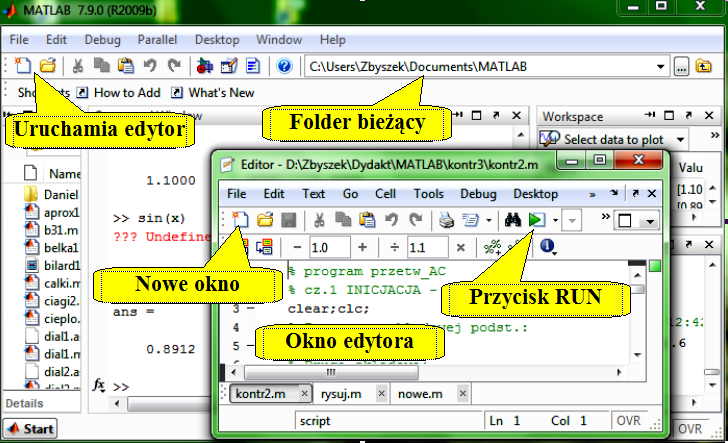
Programy zawierające wiele poleceń piszemy i uruchamiamy (testujemy) w Edytorze Matlaba.
Oto potrzebne czynności:
1. Przed rozpoczęciem pisania programów trzeba:
- założyć na dysku swój folder dla programów
- jeśli ścieżka do niego nie jest widoczna pod menu głównym Matlaba to trzeba kliknąć przycisk z trzema kropkami [...] i znaleźć ten nasz folder aby został ustawiony jako folder bieżący.
czyli Current Directory
2. Otworzyć EDYTOR MATLABa - z Menu File-New lub File-Open lub ikonami: 
3. Wpisać (lub przekopiować) tekst programu z uwzględnieniem komentarzy.
4. Zapisać utworzony program do pliku z domyślnym rozszerzeniem nazwy ".m" i domyślnie w "folderze bieżącym" (ustawionym j.w.)
5. Uruchomić działanie programu przyciskiem RUN w edytorze (z zieloną strzałką).
6. Oglądnąć i ocenić jego wyniki i ewentualne komunikaty o błędach w Oknie Komend. Poprawić te błędy i zapisać poprawioną wersję do pliku oraz wróćić do punktu poprzedniego (czyli uruchomić ponownie).
W edytorze może być otwartych kilka programów i wtedy wybieramy je zakładkami u dołu. Program można też uruchomić przez wpisanie w oknie komend nazwy jego pliku (bez rozszerzenia)
|
Zad.6. Program rysujący wykres XY. Testowanie zmian okresu próbkowania
a) Przekopiuj poniższy program PR1 do edytora i uruchom dwukrotnie: raz dla Dx=0.4 i drugi raz dla Dx=0.04.
Który wykres jest do przyjęcia? Sformułuj wnioski z tego doświadczenia. Jak widać procedura próbkowania zachodzi w każdym programie tabelaryzacji i wykreślania funkcji.
% PROGRAM PR1
clear; clc; %Czyści pamięć i okno komend
Dx=0.4; % <<<<<<<<<< OKRES PRÓBKOWANIA
x=0:Dx:6; % wektor (ciąg) wartości x
y=exp(3-x).*cos(15*x); % wektor (ciąg) wartości y
plot(x,y,'-ro'); % wykres linią ciągłą, czerwoną (r=red), znacznik=kółko
grid on; % włączamy siatkę
text(2.2,12,['Okres próbkowania Dx=',num2str(Dx)])
title('Rola okresu próbkowania');
% opisy osi:
xlabel('x'); ylabel('y=exp(3-x).*cos(15*x)');
|
W powyższym programie od znaku % rozpoczynane są KOMENTARZE czyli objaśnienia dla czytającego program
b) Wyznacz częstotliwość drgań i częstotliwości próbkowania dla obu przypadków (objaśnienie w zielonej ramce poniżej).
W którym przypadku spełniony jest postulat twierdzenia o próbkowaniu?
|
Sygnał sinusoidalny w funkcji czasu przedstawiany jest jako funkcja: sin(ω*t)
gdzie parametr ω to prędkość kątowa w radianach na sekundę.
Wynika to z przyjęcia, że funkcja sinus powstaje jako rzut na oś pionową, długości promienia jednostkowego (R=1) obracającego się z prędkością kątową ω, więc kąt (droga kątowa) α = ω*t
Okres drgań T to czas jednego obrotu (o kąt 2π radianów) skąd prędkość kątowa: ω= 2π/T
albo ω = 2π*f gdzie f=1/T jest częstotliwością drgań
|
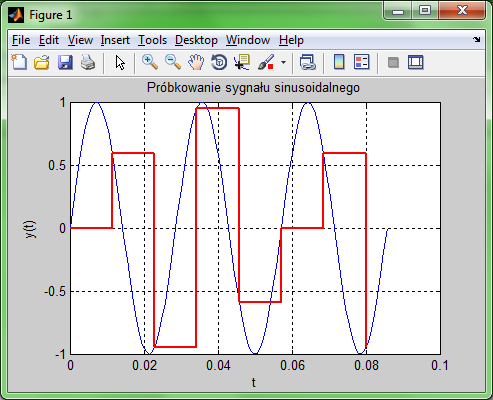
Kolejny program PR2 operuje już częstotliwościami i pozwala obserwować sygnał sinusoidalny przed i po próbkowaniu oraz uwidacznia znaczenie doboru prawidłowefo okresu próbkowania
c) Przekopiuj do edytora podany niżej program, zapisz go do pliku a następnie uruchom (przyciskiem RUN z zieloną strzałką w edytorze).
d) Obserwuj zmiany na wykresie dla kilku różnych częstotliwości fp.
% PROGRAM PR2
% Wykres k okresów sygnału sinusoidalnego
% o danej częstotliwości f, w funkcji czasu
% oraz tego sygnału po próbkowaniu z częstotliwością fp
clear; clc;
% Dane:
f=35,fp=2.5*f, k=3
T=1/f, tp=0; tk=k*T
% Wykres "dokładny" - prawie ciągły
omega=2*pi*f, n=100; dt=(tk-tp)/n
t=0:dt:tk; y=sin(omega*t);
% Wykres liniowy "dokładny"
plot(t,y); % wykres
grid on; % siatka
hold on % pozwoli wstawić drugi wykres
title('Próbkowanie sygnału sinusoidalnego');
xlabel('t'); % opis osi x
ylabel('y(t)'); % opis osi y
% ==== Próbkowanie:
Dtp=1/fp, tt=0:Dtp:tk;
% Wykres schodkowy po próbkowaniu
L2=stairs(tt,sin(omega*tt),'r');
% pogrubiam linię:
set(L2,'LineWidth',2);
hold off
|
|
7. Program z elementami Graficznego Interfejsu Użytkownika (GUI)
|
Aplikacje graficzne w Matlabie można tworzyć w oknach graficznych (figure) albo przy pomocy poleceń programu albo przy wykorzystaniu kreatora zwanego GUIDE. My wykorzystamy pierwszy sposób, objaśniony na prostym przykładzie aplikacji zawierającej tylko suwak (slider) i napis (text).
Okno figure i tworzone w nim elementy to OBIEKTY. Funkcje tworzące obiekty graficzne pozwalają określać ich CECHY. Mają one następującą postać:
uchwyt = obiekt('Cecha1', Wartość1, 'Cecha2', Wartość, ...)
Przy tworzeniu obiektu powstaje jego identyfikator zwany uchwytem, który trzeba zapamiętać w zmiennej na
przykład F1:
>>F1=figure('Position',[5 40 790 300], 'Name', 'TESTOWANIE');
Cechy obiektu o znanym uchwycie można sprawdzać i pobierać ich wartości przy pomocy funkcji zm=get(uchwyt, 'Nazwa_cechy')
oraz modyfikować (ustawiać) przy pomocy funkcji set(uchwyt, 'Nazwa_cechy', wartosc_cechy) np.:
>> kolor_formatki=get(F1,'Color');
>> set(F1,'Color','Red');
Obiekty mogą reagować na określone ZDARZENIA, wywołując procedurę określoną wartością cechy callback.
Przyciski, suwaki, listy rozwijalne i in. elementy dialogowe zwane "kontrolkami" można tworzyć przy pomocy polecenia uicontrol (od: User Interface Control element - element sterujący interfejsu użytkownika). Rodzaj kontrolki określa cecha 'Style' obiektu uicontrol. Tą i inne ważniejsze cechy objaśnia tabela:
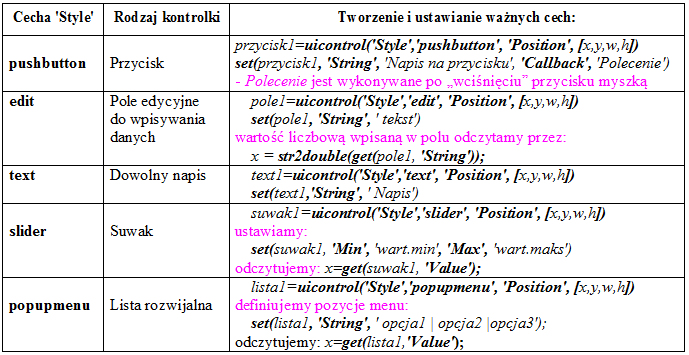
Oprócz podanych wyżej jest jeszcze wiele innych cech. Oto niektóre częściej stosowane:
'BackgroundColor', [r g b] - kolor tła - wartości barw składowych [red green blue]
'ForegroundColor', [r g b] - kolor tekstu - wartości barw składowych [red green blue]
'FontName', 'nazwa' - nazwa czcionki
'FontSize', n - rozmiar czcionki
'Position', [Xp, Yp, Dx, Dy] - położenie dolnego lewego rogu i rozmiar
'Units', 'normalized' - jednostki dla określenia położenia domyślnie 'pixels',
jeśli 'normalized' - to lewy dolny róg formatki
ma współrzędne (0,0) a prawy górny (1,1).
|
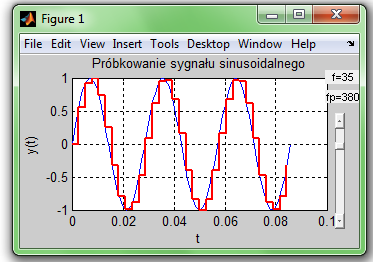
Zad.7. Uzupełnienie poprzedniego programu o suwak zmieniający częstotliwość próbkowania fp.
Dopisz (przekopiuj) na końcu poprzedniego programu podane niżej polecenia, definiujące jeszcze 2 napisy i suwak a następnie zapisz do pliku jako program PR3:
% PROGRAM PR3
%===
% ....
% TU JEST POPRZEDNI PROGRAM
% ....
%--- Pole tekstowe dla f:
T1=uicontrol('Style','Text','Units','Normalized','Position',[0.9 0.85 0.1 0.07]);
set(T1,'String',['f=',num2str(f)]);
%--- Pole tekstowe dla fp:
T2=uicontrol('Style','Text','Units','Normalized','Position',[0.9 0.75 0.1 0.07]);
set(T2,'String',['fp=',num2str(fp)]);
%--- Suwak zmieniający fp:
S1=uicontrol('Style','Slider','Units','Normalized','Position',[0.93 0.1 0.03 0.6]);
set(S1,'Value',60,'Min',50,'Max',450,'SliderStep',[0.01 0.1], 'Callback','rysuj2');
%=============
|
|
Jak widać ruch suwaka oprócz zmiany fp wywołuje procedurę rysuj2 - dzięki wartości cechy Callback.
W oknie edytora utwórz nowy pusty dokument (kliknij ikonę pustej kartki) i przekopiuj to co niżej oraz zapisz
do pliku o nazwie rysuj2.
%rysuj2
fp=get(S1,'Value');
Dtp=1/fp; tt=0:Dtp:tk;
set(L2,'XData',tt,'YData',sin(omega*tt));
set(T2,'String',['fp=',num2str(fp)]);
|
Uruchom program PR3 (musisz wybrać jego zakładkę w edytorze) i sprawdź działanie suwaka.
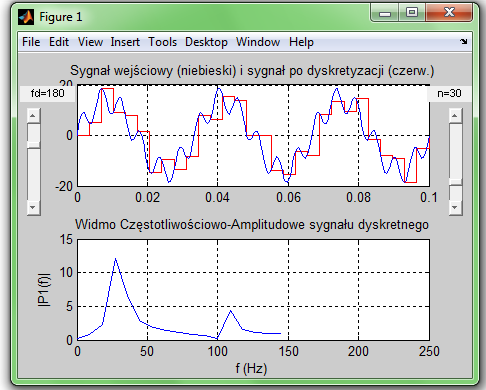
8. Obserwowanie procesu próbkowania oraz zjawiska alisingu z zastosowaniem funkcji FFT (szybkiej transformaty Fourier'a). - przy pomocy aplikacji graficznej w Matlabie
W zadaniu, sygnał ciągły złożony z dwu przebiegów sinusoidalnych ma regulowaną częstotliwość drugiej (wysokiej) składowej fd oraz regulowaną liczbę próbek n ustalonych w czasie obejmującym 3 okresy składowej niskiej.
Aplikacja składa się z trzech programów zapisanych do odpowiednich plików przy czym uruchamiać należy plik o nazwie przetw_AC
Zad.8.
a) Przekopiuj te 3 programy do osobnych okien dokumentów w edytorze i zapisz do odpowiednich plików.
b) Uruchom program przetw_AC
c) Dla kilku wartości fd wyznacz graniczne n nie wywołujące jeszcze zjawiska aliasingu na wykresie FFT. Przelicz n na częstotliwość próbkowania fp.
% program przetw_AC
% cz.1 INICJACJA - jednorazowa
clear;clc;
% Parametry składowej podst.:
A=14; f=30; T=1/f;
% Druga składowa:
Ad=5; fd=180;
% Czas obserwacji od tp do tk:
tp=0; tk=3*T;
% Liczba próbek:
n=40;
%----
t1=uicontrol('style','text','units','normalized','position',[0.005,0.85,0.09,0.03]);
%set(t1,'string','fd=180');
s1=uicontrol('style','slider','units','normalized','position',[0.02,0.5,0.03,0.33]);
set(s1,'Value',fd,'Min',30,'Max',230,'SliderStep',[0.01 0.05],'Callback','nowe');
%----
t2=uicontrol('style','text','units','normalized','position',[0.93,0.85,0.09,0.03]);
%set(t2,'string','n=30');
s2=uicontrol('style','slider','units','normalized','position',[0.95,0.5,0.03,0.33]);
set(s2,'Value',n,'Min',10,'Max',110,'Callback','nowe');
%----
rysuj;
|
|
% procedura rysuj
% Okres i częstotl. próbkowania:
Dtp=tk/(n-1); fp=1/Dtp;
% Numery próbek i ciąg chwil próbkowania t(i):
i=1:n; t(i)=(i-1)*Dtp;
% Ciąg próbek sygnału:
X(i)=A*sin(2*pi*f*t(i))+Ad*sin(2*pi*fd*t(i));
% Sygnał wejsciowy dokladny (ciągły):
nn=200; dt=tk/(nn-1); k=1:nn; tt(k)=(k-1)*dt;
XX(k)=A*sin(2*pi*f*tt(k))+Ad*sin(2*pi*fd*tt(k));
% Wykresy w funkcji czasu
subplot(2,1,1); L1=stairs(t(i),X(i),'r'); grid on;
hold on; L2=plot(tt(k),XX(k)); grid on; hold off;
title('Sygnał wejściowy (niebieski) i sygnał po dyskretyzacji (czerw.)');
xlim([0 tk]);
% FFT
NFFT = 2^nextpow2(n);
Y = fft(X,NFFT)/n;
ff = fp/2*linspace(0,1,NFFT/2+1);
subplot(2,1,2); L3=plot(ff,2*abs(Y(1:NFFT/2+1)));grid on; xlim([0 250]);
title('Widmo Częstotliwościowo-Amplitudowe sygnału dyskretnego')
xlabel('f (Hz)')
ylabel('|P1(f)|')
set(t1,'string',['fd=',num2str(fd)]);
set(t2,'string',['n=',num2str(n)]);
|
% procedura nowe
fd=get(s1,'Value');
n=get(s2,'Value');
rysuj
|
Jeśli chcesz w domu przećwiczyć podstawowe operacje to darmowy Freemat 3.6 możesz pobrać
TUTAJ