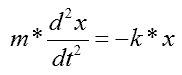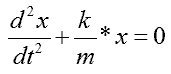Jeśli ciężar zawieszony na sprężynie wytrącimy z położenia równowagi, to oprócz równoważących się dotąd sił (ciężkości i napięcia sprężyny) zadziała na niego dodatkowa siła, proporcjonalna do wydłużenia spężyny: F = -k*x i powodująca ruch zgodnie z drugą zasadą dynamiki, czyli:

Mamy stąd równanie różniczkowe ruchu harmonicznego drgań nietłumionych:

którego rozwiązaniem jest funkcja opisująca przebieg wychyleń w zależności od czasu:

x = A * sin(omega * t +fi)

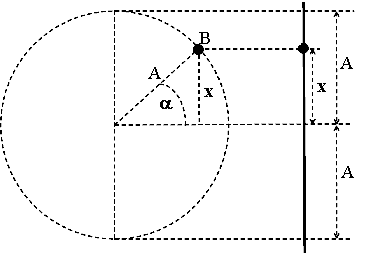
Ta sama funkcja wyraża wychylenie pionowe x punktu B, poruszającego się po okręgu ze stałą prędkością kątową omega, więc:
     - Iloczyn omega * t to kąt α,
     - A = amplituda,
     - omega = prędkość kątowa (częstość),
     - fi = faza początkowa,

Drgania harmoniczne występują także we wszystkich układach (np.: pneumatycznych, elektrycznych, hydraulicznych, akustycznych, ...) opisywanych analogicznym równaniem.