Inwersory

Jednym z głównych realnych zastosowań mechanizmów przegubowych są inwersory. Można je znaleźć m.in. w tzw. lisim ogonie czyli pile oscylacyjnej, w której ruch obrotowy silniczka jest zamieniany w ruch posuwisty wzdłuż prostej.

Mechanizm korbowy

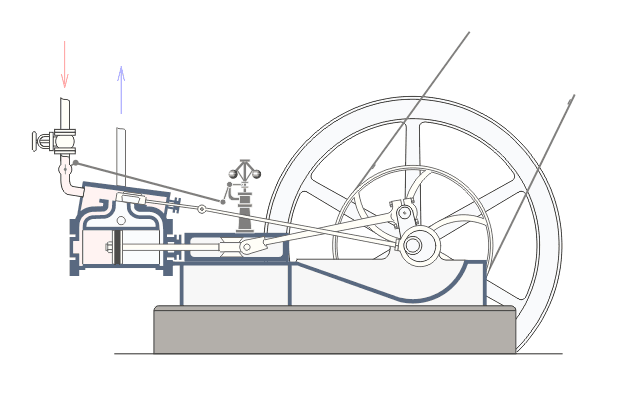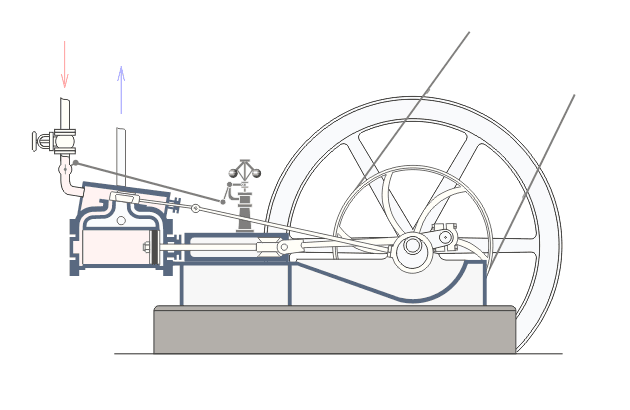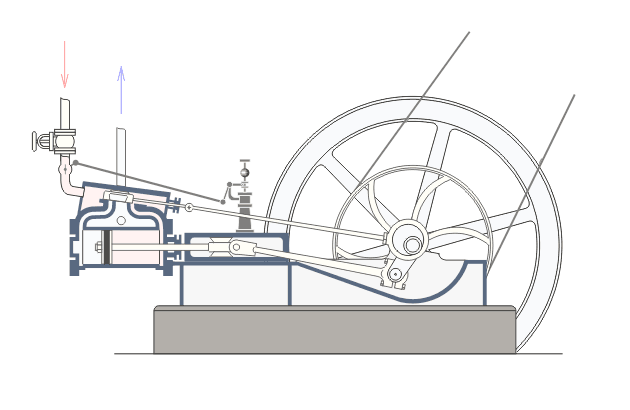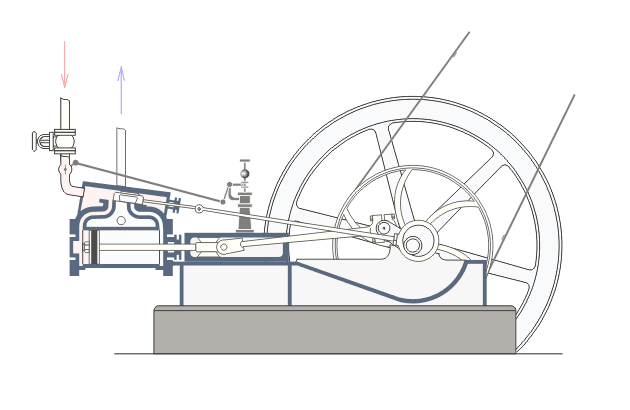Jest to najprostszy inwersor zamieniający ruch liniowy na kołowy i na odwrót. Występuje powszechnie w lokomotywach i silnikach parowych, gdzie zamienia ruch liniowy tłoka na ruch po okręgu koła.
Natomiast w aplecie obok to ruch po okręgu jest zamieniany na ruch prostoliniowy. Taka zamiana nie jest uniwersalną zasadą wśród inwersorów i nie zawsze będzie działać.

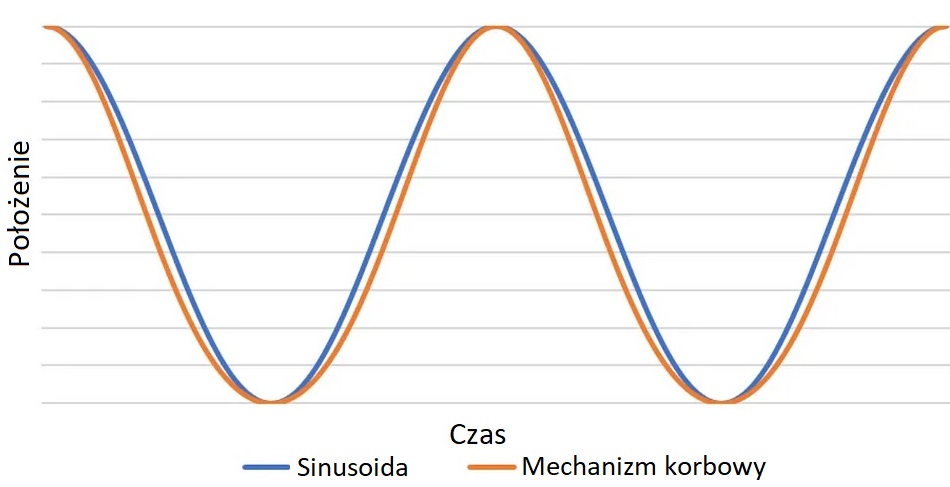
Gdyby stworzyć wykres położenia tłoka względem czasu przy stałej prędkości punktu napędzającego na okręgu spodziewalibyśmy się sinusoidy. Tymczasem wykres będzie bardzo podobny do sinusoidy jednak minimalnie różniący się od niego. Różnica ta staje się jeszcze bardziej znacząca dla wykresu prędkości i przyśpieszenia.

Inwersja względem okręgu

Najłatwiejszym dowodem, że mechanizm zamienia w sposób idealny ruch po okręgu na ruch prostoliniowy i na odwrót, jest wykazanie, że zachodzi w nim inwersja względem okręgu. Inwersja względem okręgu jest przekształceniem które przy zadanym okręgu zwanym inwersyjnym przekształca punkt węwnatrzny koła inwersyjnego na punkt zewnętrzny i na odwrót. Konstrukcja dla punktu wewnętrznego:

Wyznaczamy półprostą z środka okręgu (A) przechodzącą przez wybrany punkt (B)
Wyznaczamy przecięcie prostej prostopadłej (C) do półprostej i wybranego punktu (B)
Tworzymy styczną do okręgu inwersyjnego w punkcie przecięcia (C) i oznaczamy jej przecięcie z półprostą (D) jako inwersje wybranego na początku punktu (B).

Natomiast jeśli wybrany punkt znajduje się poza okręgiem inwersyjnym:

Wyznaczamy środek odcinka |AB| (E) i tworzymy okrąg o średnicy |AB|
W jednym z dwóch punktów przecięcia dwóch okręgów tworzymy prostą prostopadłą do odcinka |AB|. Przecięcie (D) jest inwersją punktu B.

Z relacji między kątem wpisanym a środkowym wynika że kąt ACD jest kątem prostym, a z tego możemy wywnioskować że trójkąty ACD i ACB są podobne i po prostym przekształceniu otrzymamy równanie |AD|⦁|AB| = |AC|² = r². Podobne wnioskowanie można przeprowadzić dla przypadku, gdy wybrany punkt znajduje się wewnątrz okręgu inwersyjnego. Równanie to definiuje inwersje, a co za tym dowodzi prawidłowość konstrukcji.
Zachęcam do spędzania chwili czasu na interakcje z apletem geogebry, aby lepiej zrozumieć własności inwersji.

Inwersor Peaucelliera-Lipkina

Wynaleziony w 1864r. jest najprostszy do udowodnienia zachodzącej inwersji. Aby to zrobić pokażemy, że |BC|⦁BF| = const.
|BC| = |BK| - |CK|
|BF| = |BK| + |KF| |CK| = |KF|
|BC| ⦁ |BF| = |BK|² - |CK|² = |BE|² - |EK|² - |CE|² + |EK|² = |BE|² - |CE|² = const. c.n.d.

Inwersor Hart’a

Punkty zielone i czerwone przymocowane są w połowie niebieskich ramion, tak samo jak ramie zielone. Został on wynaleziony i opublikowany przez matematyka Harrego Hart’a w 1874r. W późniejszych latach matematycy Alfred Kempe i James Joseph Sylvester uogólnili proces tworzenia tego typu inwersorów.

Inwersor Kumara-Kampling

Jest to jeden z przykładowych inwersorów jakie zaprezentowali Alfred Kempe i James Joseph Sylvester uogólniając inwersor Hart’a. Jest on o tyle ciekawy, że można w nim wyznaczyć całe ramie, które porusza się prostoliniowo. Można by wykorzystać to urządzenie do podnoszenia kubka z kawą bez straty kropli kawy.

Scotch yoke

Jest to bardzo prosty w założeniu inwersor rozwiązujący problemy mechanizmu korbowego z nie idealną charakterystyką położenia, prędkości i przyśpieszenia. Współcześnie zastosowanie znajduje w siłownikach przemysłowych tam, gdzie obchodzi się z różnymi cieczami i gazami np. w przemyśle naftowym i gazowym.

Inwersor Sarrus’a

Wynaleziony przez francuskiego matematyka Pierre Frédéric Sarrus'a (znanego m.in. za prostą metodę wyznaczania wyznaczników macierzy 3x3) w 1853 stanowił pierwszy inwersor idealnie prostoliniowy. Oprócz poważniejszych zastosowań inwersor ten znalazł również zastosowanie w zabawkach dla dzieci.

Inwersor Scott’a-Russell’a

Wynaleziony w XIX v. swą przydatność zawdzięcza prostocie w użyciu i budowie.
Napędzając go ruchem po okręgu jeden z punktów musi poruszać się po prowadnicy by mechanizm działał.

To samo a inaczej…

Jeśli zmienimy punkt napędzający, okaże się, że dodatkowa prowadnica staje się zbędna.

Inwersor Watt’a

Często ważniejszym od idealnej prostoliniowości inwersji jest prostota. W takich inwersorach nie da się wykazać inwersji matematycznej, gdyż nie zachodzi ona.
Wynaleziony już w 1784r. przez Jamesa Watt’a w patencie na silnik parowy znajduje współcześnie zastosowanie w zawieszeniu wielu pojazdów.

Kolejny inwersor Watt’a

Niewielka modyfikacja poprzedniego mechanizmu pozwoli nam otrzymać drugą równoległą inwersje, również prawie prostoliniową.

Tu powinnien być aplet geogebry... :/, jeśli go nie widzisz zmień proszę przeglądarkę.

Mechanizm Czebyszewa

Wynaleziony w XIX v. przez rosyjskiego matematyka Pafnutija Czebyszewa podchodzi do problemu inwersji w odmienny sposób od poprzednich mechanizmów. Pafnutij jako matematyk uogólnił proces tworzenia tego typu mechanizmów oraz podał równanie opisujące charakterystykę ruchu tych mechanizmów. Jego mechanizm nie znalazł niestety szerszego zastosowania w silnikach parowych, natomiast współcześnie jest wykorzystywany w niektórych dźwigach.

Mechanizm Lambda Czebyszewa

Mógłby powiedzieć, że poprzedni mechanizm był problematyczny, gdyż nie da się go bezpośrednio napędzać ruchem po okręgu. Ten mechanizm rozwiązuje ten problem a co więcej, jego prędkość na odcinku prostym jest stosunkowo stała. Jeśli wyobrazimy sobie sposób w jaki stawiamy stopę chodząc dostrzeżemy spore podobieństwo. Ze względu na charakterystykę ruchu, mechanizm ten wykorzystuje się do tworzenia tzw. stopochodów, czyli robotów które chodzą.

Mechanizm Roberts’a

Wynaleziony w XIX v. przez Richarda Roberts’a pozwala w prosty sposób otrzymać aproksymacje ruchu prostoliniowego.
Aby zobaczyć działanie mechanizmu poruszaj zielonym punktem, zaś aby zmienić długość niebieskiego ramienia przesuń suwakiem.

Drugi inwersor Hart’a

Jest to kolejny inwersor wymyślony przez Harrego Hart’a. W przeciwieństwie do poprzedniego jego wymiary są precyzyjniej określone, a choć działa dla połowy obrotu to inwersja zachodzi tylko dla ćwierć obrotu.

A jeśli by tak…

Po zamianie punktu napędzającego okaże się, że inwersja zachodzi już nie dla ćwierć a dla pół obrotu.

Szyb naftowy

Jest to jeden z najistotniejszych mechanizmów we współczesnym świecie. Dlatego wybranie odpowiednich wymiarów ramion jest kluczowe do maksymalizacji zysków, a to jak to zrobić wymaga znajomości geometrii analitycznej, trygonometrii i fizyki.
Warto zauważyć, że choć na pierwszy rzut oka może się wydawać, że w mechanizmie tym zachodzi inwersja, to tak naprawdę jej nie ma. Po przeanalizowaniu działania mechanizmu oczywistym się staje, że ruch po okręgu jest zamieniany na ruch po innym większym okręgu, ale nadal okręgu.