Zainteresowania naukowe:
TL;DR
Obliczeniowa inżynieria materiałowa, a w szczególności: trójwymiarowa rekonstrukcja mikrostruktury, modelowanie budowy i właściwości polikryształów, symulacje numeryczne.
Nieco dłużej
Rozwój przemysłu kosmicznego, energetycznego, motoryzacyjnego, zbrojeniowego, ale też wielu innych nowoczesnych branż, sprawia, że coraz intensywniej poszukiwane są nowe tworzywa mogące sprostać specyficznym wymaganiom stawianym przez projektantów i konstruktorów. Również w gałęziach przemysłu, w których jeszcze do niedawna stosowane były materiały znane od wieków – materiały tradycyjne, konkurencja na rynku wymusza stopniowe zastępowanie sprawdzonych materiałów i technologii, nowymi, mogącymi obniżyć koszty produkcji i poprawić jakość wytwarzanych produktów.
Wysoka wytrzymałość, twardość, odporność na działanie agresywnego środowiska, to naturalne cechy, które posiadają materiały ceramiczne. Ciągły rozwój tej grupy tworzyw inżynierskich, odbywa się jednak dzięki badaniom podstawowym z zakresu chemii i fizyki. Prowadzone w tych dziedzinach badania teoretyczne, pozwalają lepiej zrozumieć, wyjaśniać, a nawet przewidywać nieobserwowane dotąd zjawiska zachodzące w skali atomowej.


Również postęp w technologii chemicznej, w szczególności dotyczący syntezy nowych materiałów oraz rozwijania i optymalizacji metod i urządzeń, stosowanych w produkcji, sprawia, że uzyskiwane aktualnie tworzywa ceramiczne wykazują dużą niezawodność i trwałość.
Od wielu lat, rozwój technologiczny wynika również ze skutecznego łączenia wiedzy, zdobytej w różnych dziedzinach nauki i techniki. Wykorzystanie wielu działów fizyki, chemii, matematyki, a nawet biologii czy medycyny, w celu lepszego poznania związków miedzy budową wewnętrzną a makroskopowymi właściwościami materiałów, stanowi tradycyjnie fundament inżynierii materiałowej. W zeszłym stuleciu, takie całościowe podejście do opisu zjawisk zachodzących w materiałach w różnych skalach, umożliwiło sformułowanie szeregu podstawowych związków i wyjaśnienie ogólnych zależności decydujących o końcowych właściwościach użytkowych. W praktyce, pozwoliło to chociażby, na szerokie wykorzystanie w przemyśle materiałów kompozytowych. Dalsze, celowe prace badawcze, prowadzone w zakresie poprawy właściwości kompozytów, doprowadziły w efekcie do uzyskania i wprowadzenia na rynek nanomateriałów.
Rewolucja technologiczna, która dokonała się w ostatnim dwudziestoleciu za sprawą wzrostu mocy obliczeniowej komputerów, dostępności wysokowydajnych stacji roboczych, ale również dzięki możliwości błyskawicznego przesyłania ogromnych ilości danych poprzez sieć Internet, wpłynęła również na metody stosowane w inżynierii materiałowej. Do klasycznych specjalności wykorzystywanych w badaniach materiałowych, dołączyła również informatyka, a metody numeryczne stały się efektywnym i coraz powszechniejszym narzędziem badawczym. Aktualnie obliczeniowa inżynieria materiałowa (Computational Materials Science) zajmuje się badaniami materiałowymi w różnych skalach wymiarowych i czasowych: od analizy fundamentalnych zjawisk zachodzących w skali atomowej (metody ab initio, MD, MC), poprzez mikroskalę, w której decydującą rolę odgrywa mikrostruktura materiału (metody MD, MC, FEM, CA), aż do opisu makroskopowego, dotyczącego zachowania całych elementów konstrukcji poddawanych długotrwałemu działaniu czynników zewnętrznych (metody FEM, CE i CFD). Łączenie skal, polegające na wykorzystywaniu wyników analiz prowadzonych specyficznymi metodami w skali niższej do analiz w skali wyższej (ICME, Integrated Computational Materials Engineering), umożliwia całościowy opis zachowania materiału – jedynie w oparciu o związki konstytutywne i parametry materiałowe uzyskane poprzez symulacje. Taka koncepcja pozwala na częściowe uniezależnienie badań prowadzonych w dziedzinie inżynierii materiałowej od kosztownych, czasochłonnych i obarczonych naturalnymi niepewnościami wyników pomiarów eksperymentalnych. W przypadku poszukiwania nowych tworzyw, takie wirtualne laboratorium, w którym nieistniejący jeszcze materiał jest zarówno syntezowany” jak i badany (badania in silico), może stanowić alternatywę dla klasycznej ścieżki doświadczalnej. Podejście to, pozwala efektywnie ocenić kierunki prowadzonych poszukiwań i tym samym znacząco ograniczyć koszty dalszych badań.
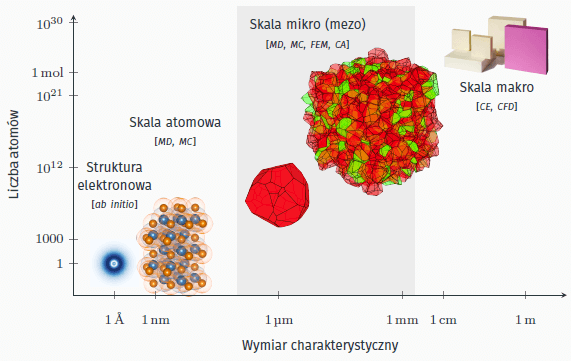
Fundamentem dla eksperymentów prowadzonych in silico jest cyfrowa reprezentacja materiału (DMR, Digital Material Representation). Powinna ona uwzględniać wszystkie istotne parametry i związki fizyczne umożliwiające symulacje analizowanych właściwości. Jednym z elementów wirtualnego materiału jest model mikrostruktury. W przypadku jedno- i wielofazowych materiałów ceramicznych – które mają budowę polikrystaliczną – rozmiar, kształt, orientacja osi krystalograficznych poszczególnych krystalitów, silnie wpływa na makroskopowe właściwości tych tworzyw. Istotne jest więc uwzględnienie zmienności cech mikrostruktury w modelu materiału. Trójwymiarowy model geometryczny, który opisuje analizowany materiał, może być zbudowany w oparciu o dane zebrane w trakcie pomiarów prowadzonych na rzeczywistym materiale (µ-CT, 3DXRD, FIB-SEM), albo może zostać wygenerowany metodami symulacyjnymi (MC, CA) bądź geometrycznymi. Często, używane w tym celu metody wzajemnie się uzupełniają – parametry uzyskane na podstawie pomiarów stanowią dane wejściowe do metod symulacyjnych czy geometrycznych.
Taka trójwymiarowa rekonstrukcja mikrostruktury jest jednym z głównych obszarów moich zainteresowań badawczych. Na podstawie analizy ilościowej, prowadzonej na obrazach losowych przekrojów próbek, stosując metody stereologiczne, staram się pozyskać informacje o trójwymiarowej budowie wewnętrznej. Informacje te wykorzystuje następnie do budowy modeli geometrycznych – wirtualnego materiału. Rekonstrukcje takie, uzupełnione informacjami o właściwościach cieplnych i mechanicznych faz składowych oraz o związki konstytutywne opisujące oddziaływania wewnętrzne, pozwalają również na prowadzenie symulacji mikromechanicznych. Stanowi to kolejny obszar mojej aktywności naukowobadawczej. Wyniki takich symulacji uzupełniają dane doświadczalne i tym samym umożliwiają głębsze zrozumienie zjawisk obserwowanych w mikroskali, które decydują o makroskopowych właściwościach materiałów ceramicznych.


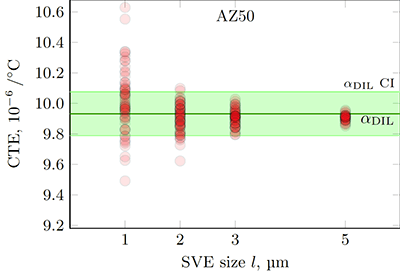
Jakość wyników uzyskiwanych metodami numerycznymi poprzez symulacje prowadzone na dwu- lub trójwymiarowych modelach mikrostruktury, zależy jednak zarówno od parametrów opisujących materiał, zastosowanych równań konstytutywnych (modelu materiałowego), jak również od rozmiaru analizowanej przestrzeni. Podobnie jak w przypadku pomiarów doświadczalnych, wykonywanych na rzeczywistych próbkach materiału, istotna jest reprezentatywność. W metodach obliczeniowych, rozmiar przestrzeni zapewniający uzyskanie właściwości efektywnych, czyli odpowiadających mierzonym parametrom makroskopowym, określany jest jako reprezentatywny element objętościowy (RVE, Representative Volume Element). W praktyce, dla materiałów polikrystalicznych, których krystality wykazują anizotropię wynikającą z symetrii sieci krystalograficznej, rozmiar takiego elementu powinien być bardzo duży. Aby przyspieszyć obliczenia i ułatwić analizę uzyskanych danych, RVE zastępuje się zestawem wielu mniejszych elementów, które łącznie stanowią statystycznie równoważny element objętości (SVE, Statistical Volume Element). Liczebność takiego zestawu zależy oczywiście od rozmiaru pojedynczej realizacji (niezależnego elementu, na którym prowadzona jest symulacja), ale również od właściwości faz składowych, a w szczególności anizotropii poszczególnych krystalitów składających się na pojedynczą realizację. Temat ten jest aktualny i istotny w dziedzinie obliczeniowej inżynierii materiałowej. Składają się na niego elementy statystyki, analizy danych, ale też aspekty czysto praktyczne, związane z ograniczeniami wynikającymi z dostępnej mocy obliczeniowej. Dlatego jest to dla mnie kolejne interesujące zagadnienie, którym zajmuje się w ramach pracy naukowej.
Specyfika właściwości materiałów ceramicznych, wynikająca chociażby z małej plastyczności, niskiego przewodnictwa cieplnego, czy obecności porów, sprawia, że występujące w tej grupie materiałów zjawiska są często trudne do analitycznego opisu. Kruche pękanie, czy obecność resztkowych naprężeń cieplnych, mogących wywoływać w materiale mikrospękania, są zależne od lokalnej konfiguracji – ułożenia krystalitów i obecności wad krytycznych. Dodatkowo są zjawiskami silnie nieliniowymi. Ich stochastyczna natura sprawia, że nadal poszukiwane są modele mogące z zadowalającą dokładnością i precyzją, pozwolić na przewidywanie makroskopowych właściwości tworzyw ceramicznych. Z tego względu ciekawe jest obserwowanie, analizowanie i uczestnictwo w badaniach prowadzonych dla lepszego poznania tej grupy tworzyw.
