Zagadnienia matematyczne

Liczba Shannona

Popularnym faktem naukowym jes to że, ilość kombinacji szachownicy jest większa niż Liczbą kombinacji szachowych jest nazywana liczbą shannona. - 10¹²⁰. Wartość została określona na podstawie obserwacji partii szachowych w których było około 30 możliwości na każdy ruch i 80 posunięć - 30⁸⁰. wyprowadził tę liczbę by udowodnić, że komputer nie jest w stanie przeanalizować każdego możliwego ruchu, ponieważ w momencie gdy obliczałby jedną grę na mikrosekundę zajęłoby mu to czas do końca wszechświata by dokończyć obliczenia. Jednakże jeżeli chcielibyśmy ograniczyć te kombinacje do tych racjonalnych - czyli tych w których dwóch zawodników chce wygrać, liczba kombinacji wynosiłaby około 10⁴⁸. W swojej książce "Chess Metaphors" Diego Rasskin-Gutman wskazuje, że gracz, który rozpatruje osiem ruchów w przód, wyobraża sobie tyle gier, ile jest gwiazd w galaktyce.

Liczba ruchów	Liczba możliwych kombinacji
1	20
2	400
3	8,902
4	197,281
...	...
9	2,439,530,234,167
10	69,352,859,712,417

Problem skoczka szachowego

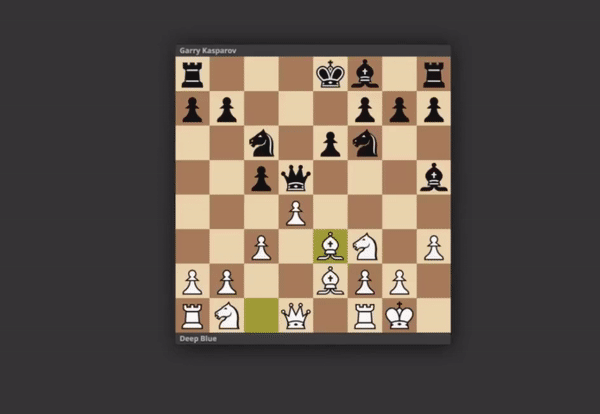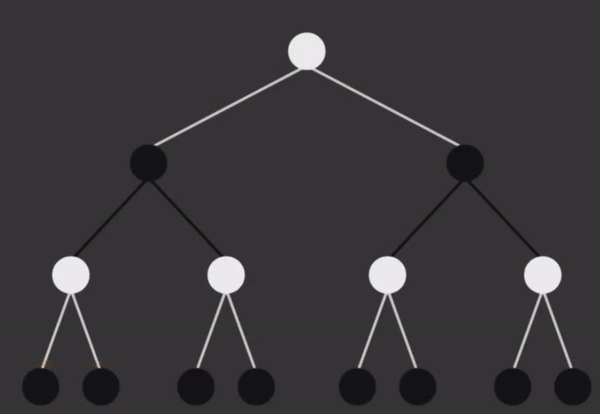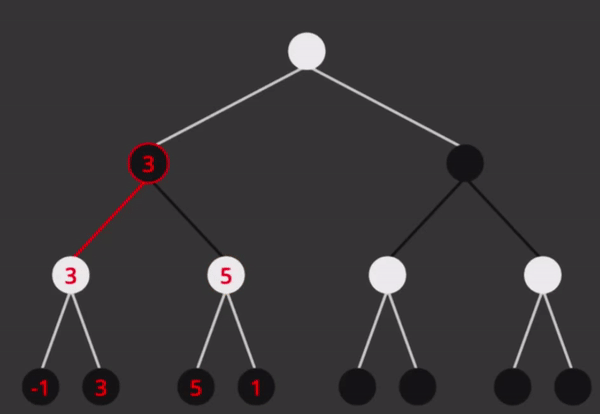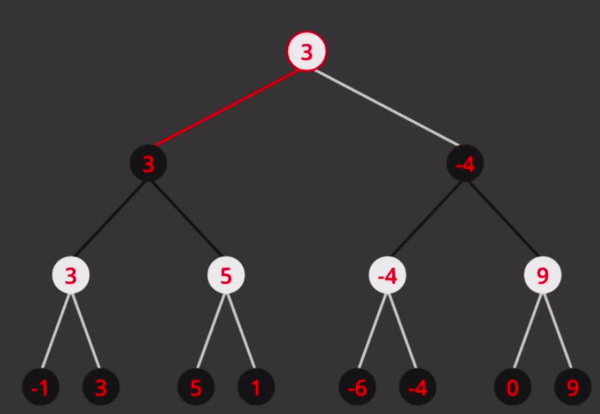
Do poprawnego rozwiązania tego problemu potrzebna jest znajomość zasady poruszania się skoczka po szachownicy - charakterystyczne "L". Istotą problemu jest, rozpoczynając z wyznaczonego pola na szachownicy, odwiedzić wszystkie pola szachownicy tak aby każde z nich było odwiedzone tylko raz. Problem intrygował matematyków od wieków np. Leonarda Eulera który pod koniec XVIII w. opracował metodę pozwalającą na rozwiązanie problemu.

Rozwiązania problemu dzielą się na: zamknięte - z końcowej pozycji figura jest w stanie dojść do początku jednym ruchem, oraz otwarte - w których nie ma takiej możliwości. Istnieje rozwiązań zamkniętych na planszy 8x8. Nie wiadomo ile istnieje rozwiązań otwartych. Dzieki postępowi technologicznemu znaleziono 140 rozwiązań . Nie istnieje żadne rozwiązanie w pełni magiczne.

Rozwiązanie zamknięte (Źródło: Numberphile)

Rozwiń rozwiązanie problemu

Wybierz pozycję startową dla skoczka. Następnie wybierając kolejno jeden z możliwych ruchów, spróbuj doprowadzić do zapełnienia całej planszy swoimi ruchami.

Rozwiązanie problemu skoczka szachowego

Poradnik krok po kroku jak rozwiązać problem metodą "Czterech diamentów".

Podział szachownicy

Możliwe diamenty

Algorytm ruchów

Istnieje wiele różnorodnych sposobów na rozwiązanie tego problemu. Niestety większość z nich wymaga zapamiętania długich kombinacji numerów lub wizualizowania skomplikowanych wzorów geometrycznych. Przedstawiony sposób pozwala na rozwiązanie tego problemu w prostych krokach, pamiętając jedynie metodę działania. Analiza tego rozwiązania pokazuje jak ważnym jest rozdzielanie dużych problemów w mniejsze z którymi łatwiej sobie poradzić.

Pierwszym krokiem do rozwiązania tego problemu jest podzielenie szachownicy na 4 kwadraty o 4 wierszach i 4 kolumnach. Każdemu nowo powstałemu kwadratowi należy przydzielić odpowiedni numer.

Do następnego kroku potrzebne jest poznanie tytułowych 'diamentów'. Są to 4 figury, możliwe do zapisania na siatce 4x4. Każda z figur jest zbudowana według zasady poruszania się skoczkiem. Gdy nałożymy wszystkie diamenty na jedną siatkę, zauważymy że wierzchołki tych figur pokrywają cały kwadrat.

Ostatnim krokiem jest przestrzeganie ściśle określonych zasad algorytmu poniżej.

Pierwszym krokiem jest wybranie dowolnego miejsca na szachownicy
Następnie sprawdzamy w którym kwadracie i diamencie znajduje się nasz skoczek
Wiedząc, że zajęcie całego diamentu jest dostępne w 3 ruchach, wybieramy kolejno 3 wierzchołki zajmowanego diamentu.

Ważna informacja!

Wybierając kierunek 'wypełniania' zajmowanego diamentu, zaplanuj to tak aby zakończyć na polu możliwie jak najbardziej oddalonym od rogów szachownicy.

Po wypełnieniu zajmowanego diamentu, skoczek powinien znajdować się na miejscu z którego jest w stanie przenieść się do tego samego typu diamentu w następnym kwadracie.
Wypełniamy pozostałe ćwiartki pierwszym diamentem.
Po wypełnieniu ostatniej ćwiartki, należy sprawdzić jakie możliwości ruchu są dostępne, wybieramy tą możliwość która znajduje się w innej ćwiartce i rozpoczynamy nowy diament.
Powtarzamy algorytm z pozostałymi diamentami, przy poprawnym wyborze pól skoczek zawsze powinien zająć wszystkie pola szachownicy

Przejdź do rozwiązywania problemu

Problem 8 hetmanów

Hetman jest najsilniejszą figurą na szachownicy. Istotą problemu jest umieszczenie 8 hetmanów tak, aby wzajemnie się nie atakowały. Carl Friedrich Gauss poświęcił temu zagadnieniu sporo czasu, czego efektem było wyszczególnienie wszystkich możliwych kombinacji. To zadanie ma . Ilość kombinacji ustawień ośmiu figur na szachownicy możemy obliczyć ze wzoru na kombinację bez powtórzeń: $$ \binom{64}{56} = {64! \over 8!\cdot(64-56)!} = 4\,426\,165\,368 $$ Posiadając te informacje wiemy, że losowo układając 8 hetmanów na szachownicy jest ${23 \over 1106541342}\%$ szansy na to, że układ będzie spełniał wymagania problemu.

Wizualizacja algorytmu rekurencyjnego szukającego rozwiązania problemu 8 hetmanów
(źródło: Wikimedia commons)

Rozwiń przykładowe rozwiązanie problemu

Rozmieść 8 hetmanów tak aby żaden z nich nie atakował innego. Jeżeli uznasz, że chcesz cofnąć swój ruch kliknij na ustawionego hetmana. Zielone pola są w obszarze ataku figury.

Rozwiązanie problemu 8 hetmanów

Przykładowe rozwiązanie wykorzystujące własności symetrii.

Nie da się opisać jednym wzorem wszystkich rozwiązań problemu 8 hetmanów. Znając jedno rozwiązanie możemy przez proste transformacje wyprowadzić 8 kombinacji układów figur poprzez rotację i odbicie lustrzane. Przedstawiony sposób znacznie ułatwia zapamiętanie układu rozwiązującego to zagadnienie.

Pierwszym krokiem jest ustawienie hetmana na pole C1
Następnie ustawiamy hetmana na polu F8 które jest odbiciem lustrzanym pola pierwszego hetmana.
W celu wybrania kolejnej pozycji wyobrażamy sobie ruchy skoczka z pozycji C1
Wybieramy kombinację dwóch pól które nie są na tej samej linii.

Ważna informacja!

Wybierając pola warto zwrócić uwagę na to żeby nie kolidowały one z odpowiednikami po drugiej stronie planszy. W przypadku pokazanym na zdjęciach para B3 i E2 spełnia ten wymóg a A2 i D3 już nie.

Następne dwie figury ustawiamy na polach które są odbiciem lustrzanych poprzednich.
Pozostałe dwie figury ustawiamy na pozostałych nieatakowanych miejscach.

Przejdź do rozwiązywania problemu

Problem 4 skoczków

Ten problem matematyczno-szachowy pochodzi z książki "Algorithmic Puzzles" autorstwa Anany Levitin oraz Marii Levitin. Problem czterech skoczków jest często stosowany na rozmowach rekrutacyjnych by sprawdzić radzenie sobie z problemami i technikę rozwiązywania. Na rogach planszy 3x3 rozstawiono cztery skoczki. Istotą problemu jest przeniesienie każdej figury na przeciwny narożnik planszy za pomocą ruchu skoczka i oszacowanie jaka będzie najmniejsza możliwa liczba ruchów doprowadzająca do rozwiązania problemu. Sposób rozumowania metodą grafów:

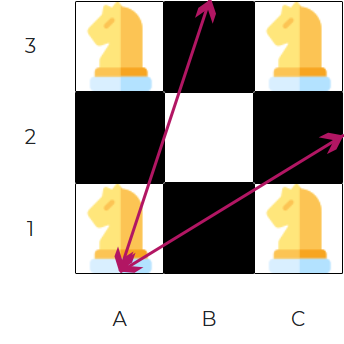
Jednym z założeń zadania jest to, że będziemy poruszali się skoczkami zgodnie z zasadami szachowymi. W początkowej fazie od każdego skoczka prowadzimy możliwe ruchy.

Krok 1/4

Liczba ruchów: 0 Za pomocą interaktywnej planszy oblicz ile ruchów jest potrzebnych by przenieść każdego ze skoczków na przeciwny narożnik. By wybrać figurę którą chcesz zrobić ruch kliknij na nią. Po najechaniu na skoczka wyświetli się pole na którym powinien skończyć rozgrywkę.

Algorytm Minimax

Ten algorytm jest powszechnie wykorzystywany w programach grających w szachy. Polega na sprowadzeniu aktualnego układu szachownicy do jednej opcji, z której możemy przejść do wielu następnych. Algorytm często wizualizowany jest jako drzewo binarne, w którym każdy punkt reprezentuje wybrane ułożenie figur na szachownicy, a jego wartość jest wyrażana w zależności od ustalonych priorytetów programu (Najczęściej ilość figur białych i czarnych na szachownicy). Ten algorytm jest wykorzystywany w grach, gdzie i gdzie ruchy następują naprzemiennie.

Algorytm wykorzystuje rekurencję by oznaczyć wartości kolejnych wierzchołków drzewa binarnego. Znając wartości poszczególnych układów na wyznaczonej warstwie, w zależności od tego który gracz ma wtedy ruch, może wybrać najkorzystniejszą krawędź dla niego. Powtarzając tę czynność dla każdej warstwy, w początkowym punkcie drzewa gracz będzie w stanie określić ścieżkę, zgodnie z którą powinien rozgrywać partię by osiągnąć najlepszy wynik.