
Mamy klatkę przestrzenną, która jest trójwymiarową szachownica. Zwykła szachownica ma 82 = 64 pól kwadratowych, szachownica przestrzenna ma 83 = 512 "klatek".
Tematem zadania jest umieszczenie 64 wież w 64 klatkach spośród 512 tak, żeby żadna wieża nie biła innej. Ruch wieży jest taki sam jak na normalnej szachownicy ale dodatkowo w dodatkowej osi (góra-dół). Wieże umieść tak aby niemożliwe było umieszczenie 65-ej wieży bez narażenia jej na bicie ze strony ustawionych wież.
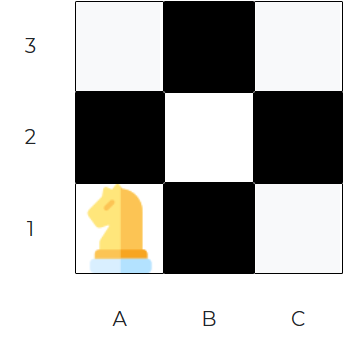
Ustawiamy skoczka w rogu szachownicy 3x3 tak jak na obrazku. Jak dużo różnych pól jest w stanie odwiedzić skoczek w 3 ruchach.
Znając zasady poruszania się wieży po szachownicy, oblicz ile maksymalnie wież może być równocześnie na planszy żeby żadna z nich się nie atakowała.
Dana jest szachownica 8x8, której pola pokolorowane są w tradycyjny sposób. W jednym ruchu zmieniamy kolory pól w wybranym wierszu lub kolumnie: czarne kola zmieniają kolor na biały, a białe na czarny. Udowodnij, że nie istnieje taka liczba ruchów która doprowadziłaby do stanu w którym szachownica ma tylko jedno pole czarne.
Na każdym polu szachownicy 10x10 napisano jedną z liczb 1,2, ... ,10. Okazało się, że każde dwie liczby napisane na polach mających wspólny bok lub wspólny wierzchołek są względnie pierwsze. Wykaż, że pewna liczba występuje na szachownicy co najmniej 17 razy.
Według legendy, mędrzec który wynalazł szachy tak zachwycił grą swojego władcę, że mógł sobie wybrać nagrodę. Ten niemyśląc długo poprosił o liczbę ziaren pszenicy, którą wyznaczy szachownica w następujący sposób:
Na pierwszym polu położono 1 ziarno i na każdym kolejnym polu podwajając liczbę z poprzedniego. Oblicz ile ziaren pszenicy był winny władca swojemu poddanemu, jeżeli szachownica ma 64 pola.
Na szachownicy 9x9 ustawiono 9 wież w taki sposób, że żadne dwie figury się nie atakują. Następnie każdą wieżę przestawiono na inne pole ruchem skoczka. Wykaż, że po tym ruchu będzie przynajmniej jedna para wież które się będą atakować.

W każde pole tablicy o wymiarach 25x25 wpisano liczbę 1 lub -1. Następnie dla każdego wiersza i każdej kolumny obliczono iloczyn wszystkich liczb stojących w danym wierszu lub danej kolumnie. Wykaż, że suma 50 uzyskanych iloczynów jest różna od 0.
Grasz rozgrywkę szachową z doświadczonym przeciwnikiem. W każdej grze masz 75% szany, że gra zakończy się remisem. W pozostałych grach jest \({2 \over 3}\) szansy, że wygrasz i \({1 \over 3}\), że przegrasz.
Pierwszy zawodnik który wygra dwie gry z rzędu jest nazywany zwycięzcą. Jakie jest prawdopodobieństwo, że to ty wygrasz rozgrywkę?