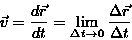
Mechanika klasyczna to jeden z najlepiej znanych działów fizyki. Jest to również dział, którego osiągnięcia znalazły szerokie zastosowanie w życiu codziennym. Podstawy teoretyczne zostały sformułowane w 1687 r przez wybitnego fizyka i matematyka Izaaka Newtona, jednego z ojców fizyki klasycznej. W pracy Philosophiae Naturalis Principia Mathematica sformułował podstawy fizyki klasycznej (zasady dynamiki Newtona) i przedstawił ich zastosowanie w zagadnieniach mechaniki, astronomii i fizyki. Sformułował również prawo powszechnego ciążenia (prawo grawitacji Newtona).
Prawa Newtona uzupełnione są zasadą zachowania pędu i zasadą zachowania energii mechanicznej. Dodatkowo stosuje się prawo dynamiki dla brył sztywnych, będące odpowiednikiem II zasady dynamiki Newtona.
Prędkość (liniowa, chwilowa) jest wielkością wektorową definiowaną poprzez stosunek przemieszczenia do (bardzo krótkiego) czasu, w którym to przemieszczenie nastąpiło
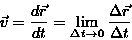
Przyspieszenie (liniowe, chwilowe) jest wielkością wektorową definiowaną poprzez stosunek zmiany prędkości do (bardzo krótkiego) czasu, w którym ta zmiana nastąpiła
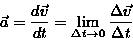
Prędkość kątowa (chwilowa) jest wielkością wektorową definiowaną poprzez stosunek zakreślonego (skierowanego) kąta do (bardzo krótkiego) czasu, w którym ta zmiana nastąpiła
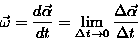
Przyspieszenie kątowe (chwilowe) jest wielkością wektorową definiowaną poprzez stosunek zmiany prędkości kątowej do (bardzo krótkiego) czasu, w którym ta zmiana nastąpiła
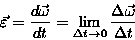
Opuszczenie w powyższych czterech definicjach fragmentów "bardzo krótkiego" zamienia definicje wielkości kinematycznych chwilowych na średnie.
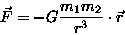
Jeżeli siły działające na punkt materialny równoważą się, to w inercjalnym układzie odniesienia ciało porusza się ruchem prostoliniowym jednostajnym lub spoczywa.
Zmiana pędu ciała jest równa popędowi działającej na nie wypadkowej siły F
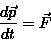
Jeśli ciało A działa na ciało B siłą F, to B działa na A siłą o tej samej wartości i kierunku, lecz o przeciwnym zwrocie (zasada akcji i reakcji).
Dla ciał o stałej masie II zasada dynamiki Newtona ujmowana jest w postaci równania
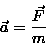
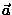 - przyspieszenie,
- przyspieszenie,
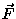 - wypadkowa działająca siła.
- wypadkowa działająca siła.
Równanie
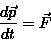
Zasady dynamiki Newtona są fundamentem klasycznej fizyki. W świetle mechaniki kwantowej i teorii względności okazały się prawami przybliżonymi.
W układach odosobnionych całkowity wektorowy pęd układu jest stały.
Podczas ruchu pod działaniem sił zachowawczych energia mechaniczna (suma energii kinetycznej i potencjalnej) pozostaje stała. Siłę nazywamy zachowawczą jeśli jest ona funkcją jedynie położenia (wektora wodzącego) r cząstki: F=F(r) taką, że praca tej siły przy przesunięciu cząstki o wektor dr da się wyrazić w postaci: dW=F dr. Praca wykonana przez siłę zachowawczą na drodze między dwoma punktami A i B zależy tylko od położenia tych punktów a nie zależy od kształtu drogi, po której porusza się ciało.
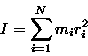
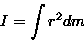
Dla ruchu obrotowego odpowiednikiem drugiej zasady dynamiki Newtona w postaci uogólnionej jest
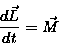
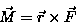
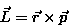
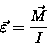
Autorzy: Marcin Mączka, Wojciech Jurek, Jakub Lipiński, Grzegorz Maczuga
 |
 |