 Punkt materialny porusza się w ten sposób, że jego położenie jest następującą funkcją czasu:
Punkt materialny porusza się w ten sposób, że jego położenie jest następującą funkcją czasu:
Fizyka dla informatyków - Notatki w InternecieMechanika - zadania |
 Punkt materialny porusza się w ten sposób, że jego położenie jest następującą funkcją czasu:
Punkt materialny porusza się w ten sposób, że jego położenie jest następującą funkcją czasu:
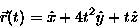
 Ciało wyrzucono pod kątem
Ciało wyrzucono pod kątem 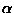 do poziomu z prędkością v0.
Zaniedbując opór powietrza i przyjmując wartość przyspieszenia ziemskiego g, znaleźć:
do poziomu z prędkością v0.
Zaniedbując opór powietrza i przyjmując wartość przyspieszenia ziemskiego g, znaleźć:
Odpowiedź:
 Pokazać, że w ruchu jednostajnie przyspieszonym droga przebyta przez ciało wyraża się znanym wzorem:
Pokazać, że w ruchu jednostajnie przyspieszonym droga przebyta przez ciało wyraża się znanym wzorem:
 Pokazać, że pod wpływem siły proporcjonalnej do wychylenia ale przeciwnie skierowanej położenie ciała zmienia się sinusoidalnie w czasie.
Pokazać, że pod wpływem siły proporcjonalnej do wychylenia ale przeciwnie skierowanej położenie ciała zmienia się sinusoidalnie w czasie.
Wskazówka:
 Rozwiązać problem wahadła matematycznego dla małych wychyleń.
W szczególności rozwiązać równanie ruchu i znaleźć okres drgań wahadła.
Rozwiązać problem wahadła matematycznego dla małych wychyleń.
W szczególności rozwiązać równanie ruchu i znaleźć okres drgań wahadła.
Odpowiedź:gdzie: l - długość wahadła, m - masa ciała zawieszonego na końcu nici, F - siła działająca na ciało (styczna do toru)
 Po rzece płynie łódka ze stałą względem wody prędkością v1, prostopadłą do kierunku prądu.
Woda w rzece płynie wszędzie równolegle do brzegów, ale wartość jej prędkości zależy od odległości od brzegów i dana jest wzorem:
Po rzece płynie łódka ze stałą względem wody prędkością v1, prostopadłą do kierunku prądu.
Woda w rzece płynie wszędzie równolegle do brzegów, ale wartość jej prędkości zależy od odległości od brzegów i dana jest wzorem:
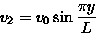
Odpowiedź:
 Znaleźć składowe przyspieszenia
Znaleźć składowe przyspieszenia 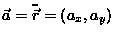 w biegunowym układzie współrzędnych
w biegunowym układzie współrzędnych 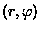 , gdzie:
, gdzie: 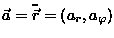
Odpowiedź:
 Znaleźć tor po jakim w płaszczyźnie xy leci ze stałą prędkością v samolotem ponaddźwiękowym pilot, który chce, aby jego koledzy stojący na lotnisku usłyszeli w tym samolocie huk silnika z całego toru.
W chwili t=0 samolot znajdował się w odległości r0 od punktu, w którym stoją jego koledzy a wektor położenia
Znaleźć tor po jakim w płaszczyźnie xy leci ze stałą prędkością v samolotem ponaddźwiękowym pilot, który chce, aby jego koledzy stojący na lotnisku usłyszeli w tym samolocie huk silnika z całego toru.
W chwili t=0 samolot znajdował się w odległości r0 od punktu, w którym stoją jego koledzy a wektor położenia 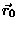 tworzył kąt
tworzył kąt 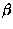 z płaszczyzną poziomą.
z płaszczyzną poziomą.
Odpowiedź:
 Punkt o masie m porusza się pod wpływem siły centralnej po torze w kształcie okręgu o promieniu R który przechodzi przez centrum działania siły (rysunek).
Jak zależy wartość tej siły od odległości od centrum?
Punkt o masie m porusza się pod wpływem siły centralnej po torze w kształcie okręgu o promieniu R który przechodzi przez centrum działania siły (rysunek).
Jak zależy wartość tej siły od odległości od centrum?
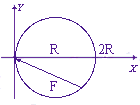
Wskazówka: ogólna metoda rowiązywania tego typu problemów polega na skorzystaniu z faktu, że siła F jest siłą centralnąoraz z tego, że moment pędu przy ruchu pod wpływem siły centralnej jest zachowany Z równania tego wynika, że Stąd otrzymujemy wzór Bineta: Aby obliczyć wartość siły należy znać równanie toru . W tym przypadku:
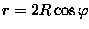
 Kula o masie m uderza w nieruchomą kulę o masie M i pozostaje w niej.
Jaka część energii kinetycznej kuli zamieni się w energię wewnętrzną (zakładamy zderzenie idealnie niesprężyste)?
Kula o masie m uderza w nieruchomą kulę o masie M i pozostaje w niej.
Jaka część energii kinetycznej kuli zamieni się w energię wewnętrzną (zakładamy zderzenie idealnie niesprężyste)?
Odpowiedź:
 Kula o masie m poruszająca się z prędkością v0 zderza się sprężyście ze spoczywającą kulą o masie M.
Przy założeniu, że zderzenie jest centralne, obliczyć prędkość i energię kinetyczną kuli o masie m po zderzeniu.
Kiedy strata energii jest największa?
Kula o masie m poruszająca się z prędkością v0 zderza się sprężyście ze spoczywającą kulą o masie M.
Przy założeniu, że zderzenie jest centralne, obliczyć prędkość i energię kinetyczną kuli o masie m po zderzeniu.
Kiedy strata energii jest największa?
Odpowiedź:Strata jest największa, gdy m=M.
 Piłeczka pingpongowa po uderzeniu o podłoge traci 1/k część swojej energii kinetycznej.
Znaleźć całkowitą drogę, jaką przebędzie piłeczka zrzucona z wysokości h, aż do chwili zatrzymania się.
Współczynik k>1.
Piłeczka pingpongowa po uderzeniu o podłoge traci 1/k część swojej energii kinetycznej.
Znaleźć całkowitą drogę, jaką przebędzie piłeczka zrzucona z wysokości h, aż do chwili zatrzymania się.
Współczynik k>1.
Odpowiedź: h(2k - 1)
 Na gładkim stole leży sznur, 1/4 długości sznura zwisa pionowo w dół.
Znaleźć czas, po którym cały sznur spadnie ze stołu na podłogę, jeżeli w chwili t = 0 jego predkość równa się zeru, a całkowita długość sznura wynosi l.
Na gładkim stole leży sznur, 1/4 długości sznura zwisa pionowo w dół.
Znaleźć czas, po którym cały sznur spadnie ze stołu na podłogę, jeżeli w chwili t = 0 jego predkość równa się zeru, a całkowita długość sznura wynosi l.
Odpowiedź: Należy rozwiązać równanie różniczkowe postaci:m - masa całego sznura, mh - masa odcinka h, przy warunkach początkowych h(0)=1/4ˇl i h'(0)=0.
 Kamień o masie m puszczono swobodnie (v0=0) do studni, w której poziom wody znajduje się na głębokości d.
Zakładamy, że kamień w powietrzu spada swobodnie, natomiast w wodzie działa na niego siła oporu proporcjonalna do prędkości:
Kamień o masie m puszczono swobodnie (v0=0) do studni, w której poziom wody znajduje się na głębokości d.
Zakładamy, że kamień w powietrzu spada swobodnie, natomiast w wodzie działa na niego siła oporu proporcjonalna do prędkości: 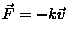 .
Znaleźć zależność położenia, prędkości i przyspieszenia kamenia od czasu.
.
Znaleźć zależność położenia, prędkości i przyspieszenia kamenia od czasu.
Odpowiedź:
 Samochód o masie m hamowany jest siłą oporu F = kv2.
Jaką drogę przebędzie samochód, zanim jego prędkość zmaleje do połowy?
Samochód o masie m hamowany jest siłą oporu F = kv2.
Jaką drogę przebędzie samochód, zanim jego prędkość zmaleje do połowy?
Odpowiedź: (m/k)ln2
 W kabinie windy zawieszono lekki bloczek przez który przerzucono nić, na końcach której zawieszono masy m1 i m2>m1.
Z jakim przyspieszeniem względem windy będą poruszać się ciężarki jeżeli:
W kabinie windy zawieszono lekki bloczek przez który przerzucono nić, na końcach której zawieszono masy m1 i m2>m1.
Z jakim przyspieszeniem względem windy będą poruszać się ciężarki jeżeli:
Wskazówka: należy skorzystać z dynamicznych równań ruchu.
 Korzystając z definicji momentu bezwładności:
Korzystając z definicji momentu bezwładności:
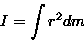
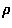 ) względem jego osi symetrii.
) względem jego osi symetrii.Odpowiedź: 1/3 ml2, 1/12 ml2, 1/2 mR2
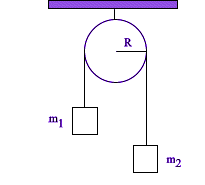
 Przez nieruchomy krążek o promieniu R przerzucono nieważką nić, na której końcach zamocowano masy m1 i m2.
Moment bezwładności krążka względem jego osi obrotu wynosi I.
Zakładamy, że nić nie może ślizgać się po krążku oraz że nie ma tarcia w jego osi.
Znaleźć przyspieszenie kątowe krążka oraz siły naciągu działające na prostoliniowe odcinki.
Przez nieruchomy krążek o promieniu R przerzucono nieważką nić, na której końcach zamocowano masy m1 i m2.
Moment bezwładności krążka względem jego osi obrotu wynosi I.
Zakładamy, że nić nie może ślizgać się po krążku oraz że nie ma tarcia w jego osi.
Znaleźć przyspieszenie kątowe krążka oraz siły naciągu działające na prostoliniowe odcinki.
|
 |
Odpowiedź:
 Na płaszczyźnie poziomej leży szpula o masie m, promieniu wewnętrznym r i zewnętrznym R.
Moment bezwładności szpulki względem jej osi symetrii wynosi
Na płaszczyźnie poziomej leży szpula o masie m, promieniu wewnętrznym r i zewnętrznym R.
Moment bezwładności szpulki względem jej osi symetrii wynosi 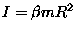 , zaś współczynik tarcia posuwistego między szpulką a płaszczyzną jest równy k.
Do końca nici przyłożono stałą siłę F.
Znaleźć wartość i kierunek przyspieszenia osi szpulki, gdy toczy się ona bez poślizgu. , zaś współczynik tarcia posuwistego między szpulką a płaszczyzną jest równy k.
Do końca nici przyłożono stałą siłę F.
Znaleźć wartość i kierunek przyspieszenia osi szpulki, gdy toczy się ona bez poślizgu.
|
|
Odpowiedź:
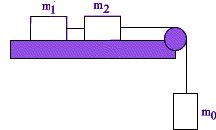
 Nieważki krążek zamocowany jest na końcu stołu.
Masy m0, m1 i m2 połączone są nieważką nicią przerzuconą przez krążek.
Zakładając, że krążek obraca się bez tarcia oraz, że masa m0 porusza się w dół znaleźć jej przyspieszenie i siłę działającą na nić łączącą masy m1 i m2, jeżeli współczyniki tarcia miedzy powierzchnią stołu a masami m1 i m2 są różne i wynoszą odpowiednio k1 i k2.
Nieważki krążek zamocowany jest na końcu stołu.
Masy m0, m1 i m2 połączone są nieważką nicią przerzuconą przez krążek.
Zakładając, że krążek obraca się bez tarcia oraz, że masa m0 porusza się w dół znaleźć jej przyspieszenie i siłę działającą na nić łączącą masy m1 i m2, jeżeli współczyniki tarcia miedzy powierzchnią stołu a masami m1 i m2 są różne i wynoszą odpowiednio k1 i k2. |
 |
Odpowiedź:
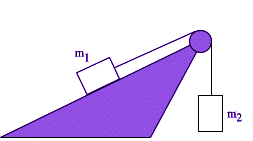
 W układzie przedstawionym na rysunku znamy kąt nachylenia
W układzie przedstawionym na rysunku znamy kąt nachylenia 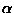 względem poziomu oraz współczynik tarcia k między tą płaszczyzną a ciałem m1.
Masę krążka i nici oraz tarcie w krążku zaniedbujemy.
Przyjmując, że w chwili początkowej obie masy były nieruchome, wyliczyć stosunek mas m2/m1, przy którym masa m2: względem poziomu oraz współczynik tarcia k między tą płaszczyzną a ciałem m1.
Masę krążka i nici oraz tarcie w krążku zaniedbujemy.
Przyjmując, że w chwili początkowej obie masy były nieruchome, wyliczyć stosunek mas m2/m1, przy którym masa m2:
|
 |
Odpowiedź:
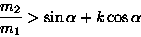
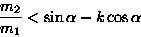
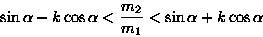
Autorzy: Marcin Mączka, Wojciech Jurek, Jakub Lipiński, Grzegorz Maczuga
 |
 |