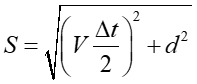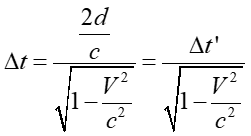Uzupełnienie - Elementy szczególnej teorii względności
• Spis treści  
• Transformacja Lorentza  
•   Transformacja Galileusza

U1.2 Dylatacja czasu

  Rozpatrzmy rakietę, w której znajduje się przyrząd wysyłający impuls światła z punktu A, który następnie odbity przez zwierciadło Z, odległe o d, powraca do tego punktu A, gdzie jest rejestrowany (rysunek U.1.2).

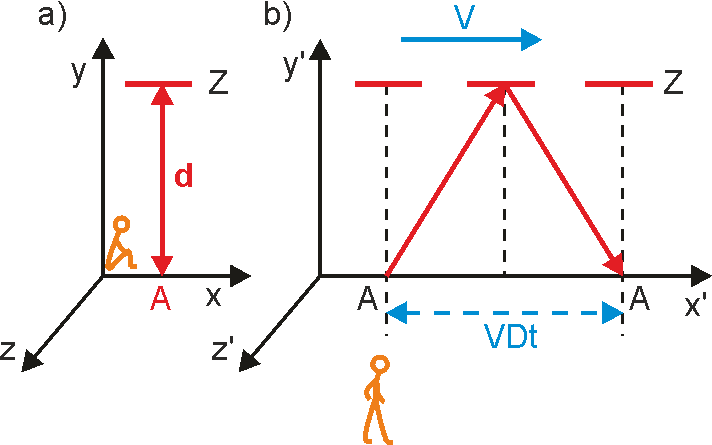
 Rys. U1.2 Pomiar czasu przebiegu impulsu świetlnego w dwóch układach odniesienia

Czas Δt ' jaki upływa między wysłaniem światła, a jego zarejestrowaniem przez obserwatora będącego w rakiecie (rysunek a) jest oczywiście równy Δt ' = 2d/c. Teraz to samo zjawisko opisujemy z układu nieruchomego obserwatora (rysunek b), względem którego rakieta porusza się w prawo z prędkością V. Chcemy, w tym układzie, znaleźć czas Δt przelotu światła z punktu A do zwierciadła i z powrotem do A. Jak widać na rysunku U1.2 (b) światło przechodząc od punktu A do zwierciadła Z porusza się po linii o długości S

Zatem czas potrzebny na przebycie drogi AZA (to jest dwóch odcinków o długości S) wynosi

Przekształcając to równanie otrzymujemy ostatecznie

Widzimy, że warunek stałości prędkości światła w różnych układach odniesienia może być spełniony tylko wtedy gdy, czas pomiędzy dwoma zdarzeniami obserwowanymi i mierzonymi z różnych układów odniesienia jest różny. W konsekwencji

To zjawisko dylatacji czasu jest własnością samego czasu i dlatego spowolnieniu ulegają wszystkie procesy fizyczne gdy są w ruchu. Dotyczy to również reakcji chemicznych, więc i biologicznego starzenia się.
Dylatację czasu zaobserwowano doświadczalnie między innymi za pomocą nietrwałych cząstek. Cząstki takie przyspieszano do prędkości bliskiej prędkości światła i mierzono zmianę ich czasu połowicznego zaniku.