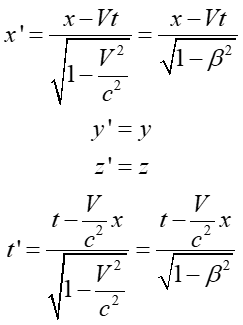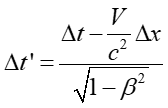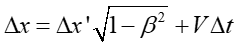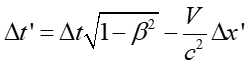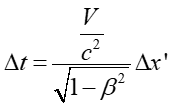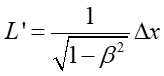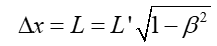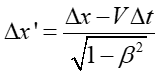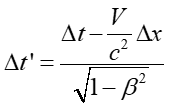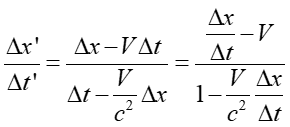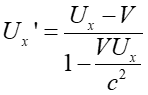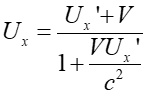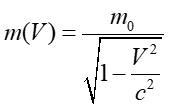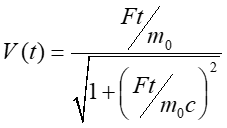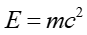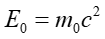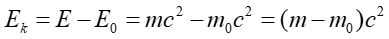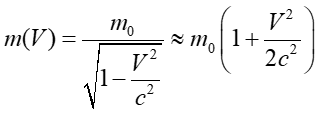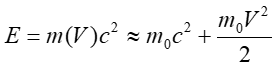Uzupełnienie - Elementy szczególnej teorii względności
• Spis treści  
• Wybrane stałe fizyczne  
•   Dylatacja czasu

U1.3 Transformacja Lorentza

  Szukamy ponownie (jak w przypadku transformacji Galileusza) wzorów przekładających spostrzeżenia jednego obserwatora na obserwacje drugiego. Chcemy znaleźć transformację współrzędnych ale taką, w której obiekt poruszający się z prędkością równą c w układzie nieruchomym (x, y, z, t), również w układzie (x ', y ', z ', t ') poruszającym się z prędkością V wzdłuż osi x będzie poruszać się z prędkością c.
Transformacja współrzędnych, która uwzględnia niezależność prędkości światła od układu odniesienia ma postać

gdzie β = V/c. Te równania noszą nazwę transformacji Lorentza. Omówimy teraz niektóre wnioski wynikające z transformacji Lorentza.

Jednoczesność

  Przyjmijmy, że według obserwatora w rakiecie poruszającej się wzdłuż osi x' (czyli także wzdłuż osi x, bo zakładamy, że te osie są równoległe) pewne dwa zdarzenia zachodzą równocześnie Δt ' = t₂ ' - t₁ ' = 0, ale w rożnych miejscach x₂' − x₁' = Δx ' ≠ 0. Sprawdźmy, czy te same zdarzanie są również jednoczesne dla obserwatora w spoczynku. Z transformacji Lorentza wynika, że

Łącząc te równania otrzymujemy związek

Jeżeli teraz uwzględnimy fakt, że zdarzenia w układzie związanym z rakietą są jednoczesne Δt ' = 0 to otrzymamy ostatecznie

Widzimy, że równoczesność zdarzeń nie jest bezwzględna, w układzie nieruchomym te dwa zdarzenia nie są jednoczesne.

Skrócenie długości

  Teraz rozpatrzmy inny przykład. W rakiecie poruszającej się z prędkością V, wzdłuż osi x ' leży pręt o długości L '. Sprawdźmy jaką długość tego pręta zaobserwuje obserwator w układzie nieruchomym.
Pomiar długości pręta polega na zarejestrowaniu dwóch zjawisk zachodzących równocześnie na końcach pręta (np. zapalenie się żarówek). Ponieważ żarówki zapalają się na końcach pręta to Δx ' = L'. Ponadto żarówki zapalają się w tym samym czasie (dla obserwatora w układzie spoczywającym) to dodatkowo Δt = 0. Uwzględniając te warunki otrzymujemy na podstawie transformacji Lorentza

gdzie Δx jest długością pręta L w układzie nieruchomym. Stąd

Okazuje się, że pręt ma mniejszą długość, jest krótszy.

Dodawanie prędkości

  W poprzednim punkcie rozważaliśmy obiekt spoczywający w rakiecie. Teraz zajmiemy się przypadkiem gdy obiekt ma już pewną prędkość U_x' w ruchomym układzie odniesienia (to jest względem rakiety). Sprawdzimy jaką prędkość U_x zarejestruje nieruchomy obserwator, w układzie którego rakieta porusza się z prędkością V wzdłuż osi x. Z transformacji Lorentza wynika, że

Dzieląc te równania przez siebie otrzymujemy

a po podstawieniu oraz

Powyższe równanie można rozwiązać ze względu na U_x

Zależność masy od prędkości

  Dotychczas zajmowaliśmy się kinematyką ruchu ciała obserwowanego z dwóch układów odniesienia poruszających się względem siebie ze stałą prędkością. Teraz chcemy odpowiedzieć na pytanie jak można opisać zachowanie ciała pod wpływem sił w sytuacji, gdy transformacja Lorentza, (a nie Galileusza) jest prawdziwa. Chodzi o to, czy druga zasada dynamiki Newtona F = dp/dt może być stosowana i czy zasada zachowania pędu ma taką samą postać we wszystkich układach inercjalnych.
Okazuje się, że warunkiem zachowania pędu przy transformacji z jednego układu odniesienia do innego jest uwzględnienie zależność masy ciała m od jego prędkości V, danej następującym wyrażeniem

w którym m₀ oznacza masę spoczynkową, czyli masę nieruchomego ciała. Zauważmy ponadto, że masa cząstki rośnie wraz z prędkością i zmierza do nieskończoności gdy V → c.

Rozpatrzmy teraz ruch ciała pod wpływem stałej siły F działającej równolegle do kierunku ruchu. Zależność prędkości ciała od czasu obliczamy na podstawie drugiej zasad dynamiki Newtona. Uwzględniając zależność masy od prędkości (U1.23) otrzymujemy

Porównanie zależność prędkości ciała od czasu działania siły w mechanice klasycznej i relatywistycznej jest pokazane na rysunku U1.3. W przeciwieństwie do opisu klasycznego, z powyższej zależności wynika, że cząstki nie da się przyspieszać w nieskończoność działając stałą siłą.

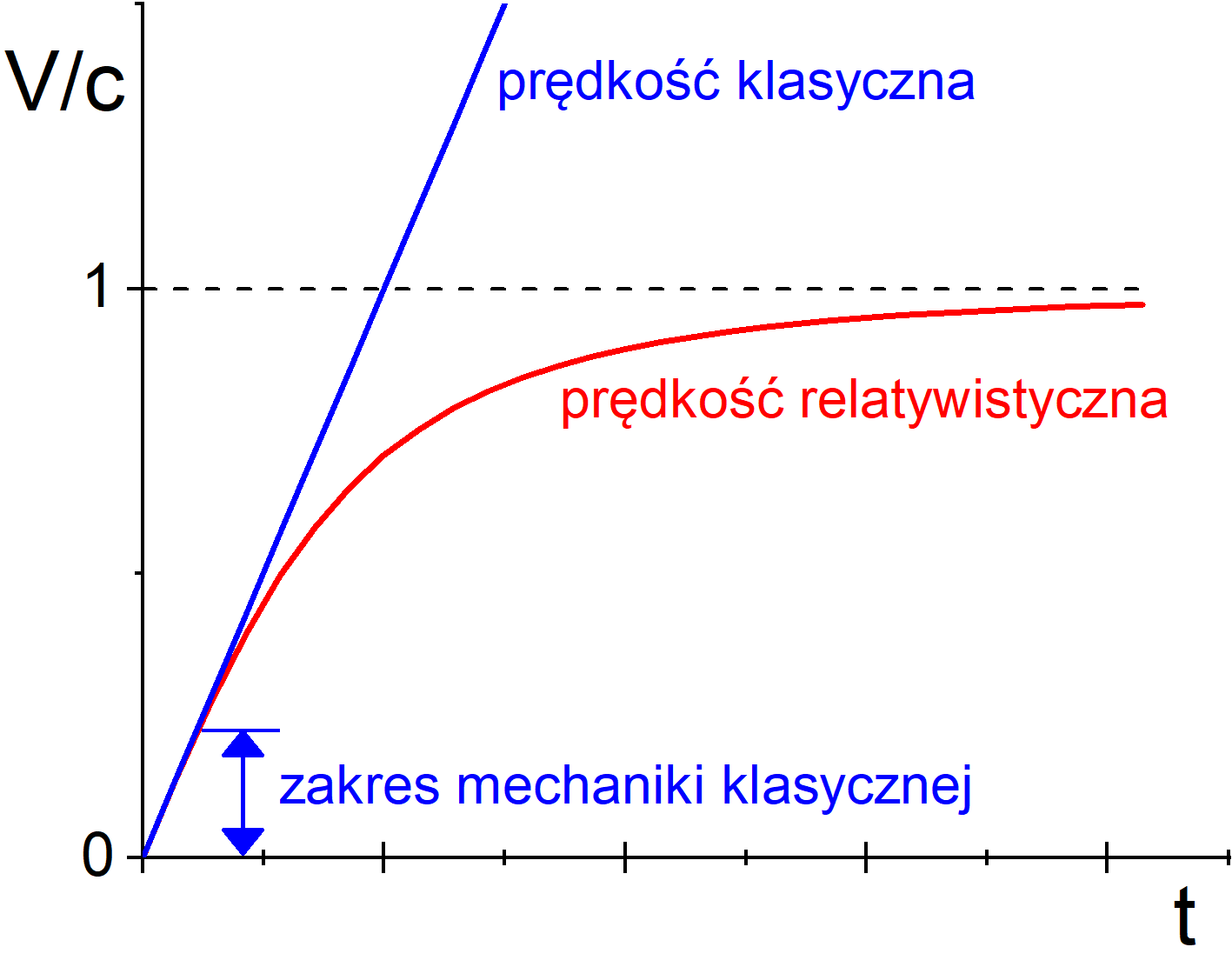
 Rys. U1.3 Zależność prędkości ciała od czasu działania stałej siły w mechanice klasycznej i relatywistycznej

Zmiana masy z prędkością została potwierdzona wieloma doświadczeniami przeprowadzonymi dla cząstek elementarnych.

Równoważność masy i energii

  Einstein pokazał, że zasada zachowania energii jest spełniona w mechanice relatywistycznej pod warunkiem, że pomiędzy masą i całkowitą energią ciała zachodzi związek

gdzie m zależy od prędkości ciała V zgodnie z równaniem (U1.23). To znane powszechnie równanie Einsteina opisuje równoważność masy i energii. Wynika z niego, że ciało w spoczynku ma zawsze pewną energię związaną z jego masa spoczynkową

Energię kinetyczną ciała poruszającego się z prędkością V obliczamy odejmując od energii całkowitej energię spoczynkową (nie związaną z ruchem)

Widzimy, że mechanika relatywistyczna wiąże energię kinetyczną z przyrostem masy ciała.

Na zakończenie zobaczmy jaką wartość przyjmuje energia całkowita, jeśli prędkość V jest mała. Dla małego V równanie (U1.23) można przybliżyć (rozwijając w szereg) do postaci

Podstawiając tę wartość do wyrażenia na energię całkowitą otrzymujemy

Pierwszy wyraz jest energią związaną z istnieniem samej masy (energia spoczynkowa) natomiast drugi jest klasyczną energią kinetyczną związaną z ruchem ciała. Otrzymaliśmy rozwiązanie klasyczne jako graniczny przypadek (dla małych prędkości) rozwiązania relatywistycznego.