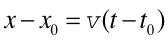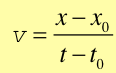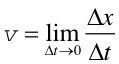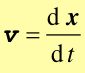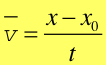2. Ruch jednowymiarowy
• Spis treści  
• Przyspieszenie  
•   Ruch jednowymiarowy, wstęp

2.2 Prędkość

Prędkość stała

  Jeżeli wskazania prędkościomierza samochodu nie zmieniają się to oznacza, że samochód porusza się ze stałą prędkością v, i jeżeli w pewnej chwili t₀ znajdował się w położeniu x₀ to po czasie t znajdzie się w położeniu x

skąd

  Zależność między położeniem x i czasem t pokazana jest na rysunku poniżej dla dwóch ciał (np. pojazdów). Jak wynika ze wzoru (2.1) nachylenie wykresu x(t) przedstawia prędkość danego ciała. Różne nachylenia wykresów x(t) odpowiadają więc różnym prędkościom. Prędkość v (wektor) może być dodatnia albo ujemna; jej znak wskazuje kierunek ruchu. Wektor v dodatni - ruch w kierunku rosnących x, ujemny to ruch w kierunku malejących x

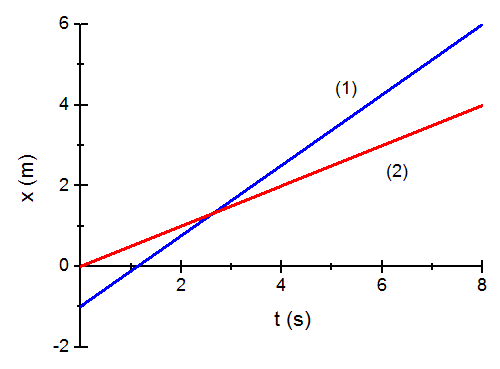
Rys. 2.1. Zależność położenia od czasu dla ciała poruszającego się ze stałą prędkością.

Prędkość chwilowa

  Gdy samochód przyspiesza lub hamuje to wskazania prędkościomierza zmieniają się i nie możemy mówić o "jednej" stałej prędkości. Prędkość zmienia się i w każdej chwili jest inna. Nie można wtedy stosować wzoru (2.1) chyba, że ograniczymy się do bardzo małych wartości x - x₀ (Δx) czyli również bardzo małego przedziału czasu Δt = t − t₀ (chwili). Prędkość chwilową w punkcie x otrzymamy gdy Δt dąży do zera

Tak definiuje się pierwszą pochodną więc

Nachylenie krzywej x(t) ponownie przedstawia prędkość v, a znajdujemy je (zgodnie z definicją pochodnej) jako nachylenie  stycznej do wykresu x(t), w danym punkcie tj. dla danej chwili t (rysunek poniżej).

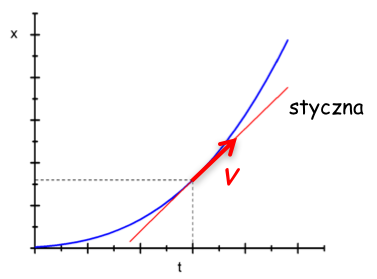
Rys. 2.2. Nachylenie krzywej x(t) jest prędkością chwilową

Prędkość średnia

   Często określenie zależności x(t) nie jest możliwe, np. przy oszacowaniu czasu dojazdu do wybranej miejscowości nie jesteśmy w stanie przewidzieć wszystkich parametrów podróży wpływających na prędkość takich jak natężenie ruchu, konieczność ograniczenia prędkości w terenie zabudowanym itp. Posługujemy się wtedy pojęciem prędkości średniej . Prędkość średnia ciała w przedziale czasu t jest zdefiniowana jako

gdzie x - x₀ jest odległością przebytą w czasie t.

Otrzymany wynik: 53.33 km/h jest różny od średniej arytmetycznej z prędkości  v₁ i  v₂, która wynosi 60 km/h.  Powodem jest to, że poszczególne wartości wchodzą w skład średniej matematycznej z różnymi czynnikami wagowymi. W naszym przykładzie obliczamy średnią względem czasu, więc skoro przedziały czasu, w których samochód jedzie z prędkościami  v₁ i  v₂ są różne to i udziały tych prędkości w średniej są też różne. Wartość średnia daje praktyczne wyniki. Zilustrujmy to jeszcze jednym przykładem:

Ten przykład wprowadza nas do omówienia przyspieszenia.