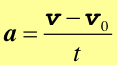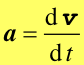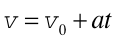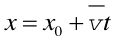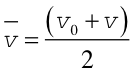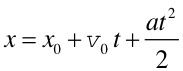Prędkość2.3 Przyspieszenie
|
Definicja Przyspieszeniem nazywamy tempo zmian prędkości. |
Przyspieszenie jednostajne
Jeżeli ciało przyspiesza lub hamuje i jego prędkość zmienia się jednostajnie z czasem to przyspieszenie a tego ciała jest stałe
|
(2.5) |
Gdy prędkość rośnie (a > 0) to ruch nazywamy jednostajnie
przyspieszonym 
, a gdy prędkość maleje (a < 0) to
ruch określamy jako jednostajnie opóźniony .
Przyspieszenie chwilowe
Jeżeli przyspieszenie nie jest stałe, zmienia się z czasem, musimy wtedy ograniczyć się do pomiaru
zmian prędkości Δv
w bardzo krótkim czasie Δt
(podobnie jak dla prędkości chwilowej). Wówczas przyspieszenie
chwilowe definiujemy jako pierwszą pochodną v
względem t.
|
Definicja |
|
(2.6) |
Ruch jednostajnie zmienny
Z ruchem jednostajnie zmiennym spotykamy się na co dzień, np. gdy obserwujemy swobodny spadek ciał w pobliżu powierzchni Ziemi. Jeżeli możemy zaniedbać opór powietrza (w porównaniu z ciężarem ciała) to każde ciało upuszczone swobodnie porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem równym 9.81 m/s2.
Wyrażenie na prędkość ciała poruszającego się ze stałym przyspieszeniem możemy otrzymać wprost ze wzoru (2.5)
|
(2.7) |
Natomiast do policzenia położenia korzystamy ze wzoru (2.4) na prędkość średnią przekształconego do postaci
|
(2.8) |
Ponieważ w ruchu jednostajnie przyspieszonym prędkość rośnie jednostajnie od v0 do v więc prędkość średnia wynosi
|
(2.9) |
Łącząc powyższe trzy równania otrzymujemy
|
(2.10) |
Jako podsumowanie, pokazane jest graficzne przedstawienie ruchu prostoliniowego jednostajnego i jednostajnie zmiennego w postaci wykresów x(t), v(t) oraz a(t).
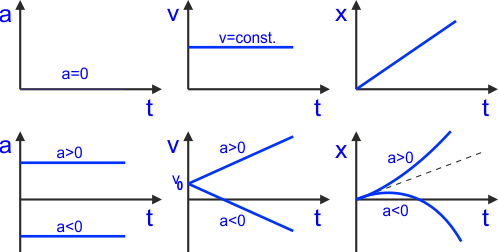
Rys. 2.3. Graficzna prezentacja ruchu prostoliniowego jednostajnego i jednostajnie zmiennego
Rozważając ruch po linii prostej możemy operować liczbami, a nie wektorami bo mamy do czynienia z wektorami równoległymi. Jednak trzeba, przy opisie zjawisk (rozwiązywaniu zadań), uświadamiać sobie, że w równaniach ruchu mamy do czynienia z wektorami. Prześledzimy to wykonując następujące ćwiczenie:
|
Ćwiczenie Dwa identyczne ciała rzucono pionowo do góry z prędkością początkową v0 w odstępie czasu Δt jedno po drugim. Na jakiej wysokości spotkają się te ciała? Sprawdź obliczenia i wynik. |
Pamiętanie o tym, że liczymy na wektorach jest bardzo istotne przy rozpatrywaniu ruchu w dwóch lub trzech wymiarach na przykład w ruchu na płaszczyźnie.