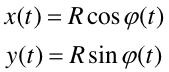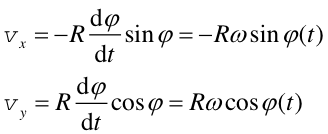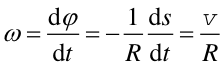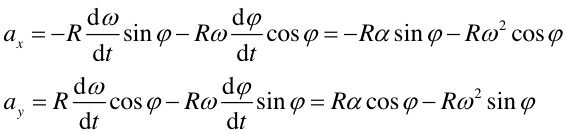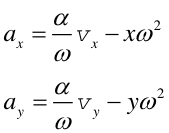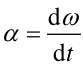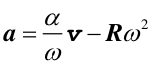Ruch przyspieszony po okręgu

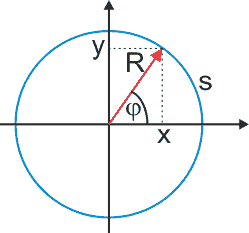
Współrzędne x, y punktu poruszającego się po okręgu można wyrazić za pomocą promienia R (o stałej wartości) oraz kąta φ (rysunek poniżej).

(1)

Przy czym związek między drogą liniową s, a drogą kątową φ , jest dany z miary łukowej kąta φ = s/R.

Różniczkując równania (1), możemy obliczyć zgodnie ze wzorami (3.1), składowe prędkości

(2)

gdzie tempo zmian drogi kątowej dφ/dt oznaczono jako prędkość kątową (analogicznie do prędkości liniowej v)

(3)

Różniczkując z kolei równania (2) otrzymamy zgodnie ze wzorami (3.1) składowe przyspieszenia

(4)

lub

(5)

gdzie wprowadzono przyspieszenie kątowe α wyrażające tempo zmian prędkości kątowej dω /dt

(6)

Na podstawie powyższych zależności możemy obliczyć wektor całkowitego przyspieszenia

(7)

Wektor przyspieszenia całkowitego a jest sumą dwóch wektorów: przyspieszenia stycznego a_s (równoległego do wektora prędkości v)

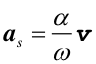
i przyspieszenia normalnego a_n (przeciwnego do wektora R czyli skierowanego do środka okręgu)

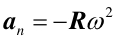
Wektory prędkości liniowej i kątowej oraz wektory przyspieszeń stycznego, normalnego i kątowego, w ruchu przyspieszonym po okręgu, są pokazane na rysunku poniżej.

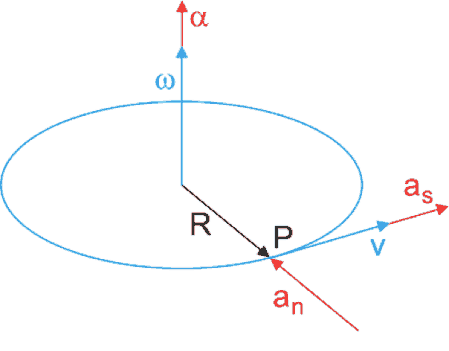
Wektory prędkości i przyspieszeń w ruchu przyspieszonym po okręgu