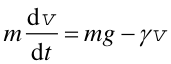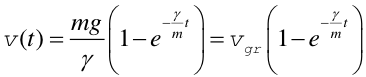Ruch w polu grawitacyjnym z uwzględnieniem oporu powietrza
Naszym zadaniem jest opisanie ruchu ciała o masie m puszczonego z pewnej wysokości nad powierzchnią Ziemi, które spadając doznaje oporu powietrza. Z codziennych doświadczeń wiemy, że opór powietrza zależy od prędkości, na przykłady podczas jazdy na rowerze, i jest tym większy im szybciej jedziemy. Przyjmiemy więc założenie, że siła oporu powietrza jest proporcjonalna do prędkości v
|
(1) |
Znak minus wskazuje, że siła oporu działa przeciwnie do kierunku ruchu (wektora prędkości v).
|
Ruch ciała odbywa się pod działaniem dwóch sił: stałej siły grawitacji i zmiennej siły oporu (rysunek obok). Wraz ze wzrostem prędkości rośnie siła oporu, aż do momentu gdy stanie się ona równa co do wartości sile grawitacji. Wówczas siła wypadkowa działająca na ciało staje się równa zeru, prędkość dalej już nie rośnie i nie rośnie też siła oporu, zgodnie z pierwszą zasadą dynamiki ciało porusza się od tej chwili ruchem jednostajnym, prostoliniowym. Graniczną prędkość vgr jaką osiąga ciało obliczamy z warunku |
|
|
(2) |
Teraz poszukujemy odpowiedzi napytanie jak zmienia się prędkość podczas ruchu. W tym celu korzystamy z drugiej zasady dynamiki Newtona, która przyjmuje postać równania
|
(3) |
Rozwiązaniem równania różniczkowego (3) jest funkcja v(t)
|
(4) |
Zależność ta jest wykreślona na rysunku poniżej. Widać, że po odpowiednio długim czasie prędkość osiąga wartość graniczną.
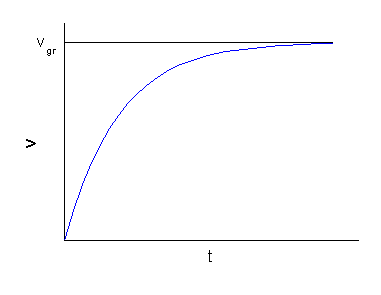
Zależność prędkości od czasu
Otrzymaliśmy więc równanie v(t) opisujące ruch ciała.


 Zasady dynamiki Newtona
Zasady dynamiki Newtona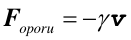

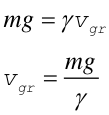
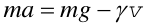 lub
lub