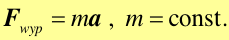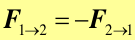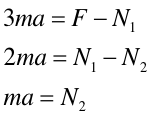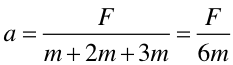4.2 Zasady dynamiki Newtona
Podstawowa teoria, która pozwala przewidywać ruch ciał,
składa się z trzech równań, które nazywają się zasadami dynamiki Newtona.
Sformułowanie pierwszej zasady dynamiki Newtona:
|
Prawo, zasada, twierdzenie Ciało, na które nie działa żadna siła (lub gdy siła wypadkowa jest równa zeru) pozostaje w spoczynku lub porusza się ze stałą prędkością po linii prostej. |
Siła wypadkowa Fwyp jest sumą wektorową wszystkich sił działających na ciało. Jeżeli Fwyp = 0 to również przyspieszenie ciała a = 0, a to oznacza, że nie zmienia się ani wartość ani kierunek prędkości tzn. ciało jest w stanie spoczynku lub porusza się ze stałą co do wartości prędkością po linii prostej. Zgodnie z pierwszą zasadą dynamiki nie ma rozróżnienia między ciałami spoczywającymi i poruszającymi się ze stałą prędkością. Nie ma też różnicy pomiędzy sytuacją gdy nie działa żadna siła i przypadkiem gdy wypadkowa wszystkich sił jest równa zeru.
Sformułowanie drugiej zasady dynamiki Newtona:
|
Prawo, zasada, twierdzenie Tempo zmian pędu ciała jest równe sile wypadkowej działającej na to ciało. Dla ciała o stałej masie sprowadza się to do iloczynu masy i przyspieszenia ciała. |
|
(4.6) |
Sformułowanie trzeciej zasady dynamiki Newtona:
|
Prawo, zasada, twierdzenie Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie. |
| (4.7) |
Pierwsza zasada dynamiki wydaje się być szczególnym
przypadkiem drugiej bo gdy a = 0 to i Fwyp = 0.
Przypisujemy jej jednak wielką wagę dlatego, że zawiera ważne pojęcie
fizyczne: definicję inercjalnego układu odniesienia ![]() .
.
|
Definicja Pierwsza zasada dynamiki stwierdza, że jeżeli na ciało nie działa żadna siła (lub gdy siła wypadkowa jest równa zeru) to istnieje taki układ odniesienia, w którym to ciało spoczywa lub porusza się ruchem jednostajnym prostoliniowym. Taki układ nazywamy układem inercjalnym. |
Układy inercjalne są tak istotne bo we wszystkich takich
układach ruchami ciał rządzą dokładnie te sama prawa. Większość
omawianych zagadnień będziemy rozwiązywać właśnie w inercjalnych układach
odniesienia. Zazwyczaj przyjmuje się, że są to układy, które spoczywają
względem gwiazd stałych ale układ odniesienia związany z Ziemią w większości
zagadnień jest dobrym przybliżeniem układu inercjalnego.
Ponieważ przyspieszenie ciała zależy od przyspieszenia układu
odniesienia (od przyspieszenia obserwatora), w którym jest mierzone więc
druga zasada dynamiki jest słuszna tylko, gdy obserwator znajduje się w układzie
inercjalnym. Inaczej mówiąc, prawa strona równania F = ma
zmieniałaby się w zależności od przyspieszenia obserwatora.
Tu dowiesz się Więcej o ... układach inercjalnych i nieinercjalnych.
Zwróćmy jeszcze raz uwagę na fakt, że w równaniu (4.6) występuje siła wypadkowa.
Oznacza to, że trzeba brać sumę wektorową wszystkich sił działających na ciało. Doświadczenia potwierdzają zasadę addytywności sił. Zasada ta dotyczy również masy: masa układu jest sumą mas poszczególnych ciał tego układu.
Prześledźmy teraz zastosowanie zasad dynamiki na następującym przykładzie.
Przykład
Rozważmy układ trzech ciał o masach 3m, 2m i m połączonych nieważkimi nitkami tak jak na rysunku poniżej. Układ jest ciągnięty zewnętrzną siłą F po gładkim podłożu. Szukamy przyspieszenia układu i naprężeń nici łączących ciała.
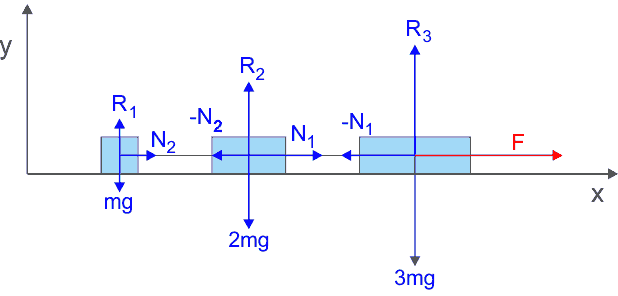
Rys. 4.2. Układ trzech mas połączonych nitkami ciągnięty siłą F
Reakcja podłoża R równoważy nacisk poszczególnych ciał tak, że siły działające w kierunku y równoważą się. Natomiast w kierunku x układ jest ciągnięty zewnętrzną siłą F, a oddziaływania są przenoszone przez nitki. Ciało o masie 3m działa na ciało o masie 2m siłą N1, a siła −N1 jest siłą reakcji na to działanie. Podobnie jest z siłami N2 i −N2. Przyspieszenie układu i siły naciągu nitek N1 i N2 obliczamy stosując drugą zasadę dynamiki Newtona do każdego ciała indywidualnie.
| (4.8) |
Sumując równania stronami otrzymujemy
| (4.9) |
Zwróćmy uwagę na addytywność mas. Taki sam wynik otrzymalibyśmy traktując ciała jak jedną masę. Doświadczenia potwierdzają zasadę addytywności masy: masa układu jest sumą mas poszczególnych ciał układu.
Podstawiając wynik (4.9) do równań (4.8) obliczamy naciągi nitek
| (4.10) |
Spróbuj teraz samodzielnie rozwiązać podobny problem.
|
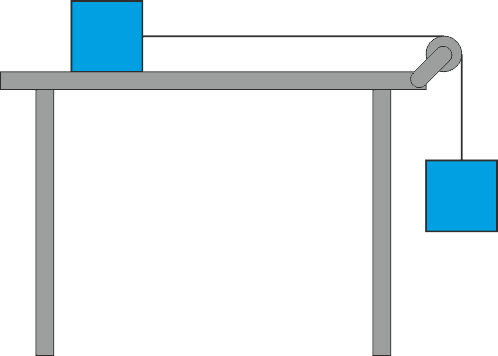
Ćwiczenie Dwa klocki o masach m1 = m2 = 1 kg są połączone nieważką nitką przerzuconą przez nieważki bloczek tak jak na rysunku poniżej. Oblicz przyspieszenie układu oraz naprężenie linki. Przyjmij, że klocek m2 porusza się po stole bez tarcia. Sprawdź obliczenia i wynik. |
Zwróćmy jeszcze raz uwagę na fakt, że w równaniu (4.6) występuje siła wypadkowa. Oznacza to, że trzeba brać sumę wektorową wszystkich sił działających na ciało. Możesz się o tym przekonać rozwiązując podane poniżej zadanie.
|
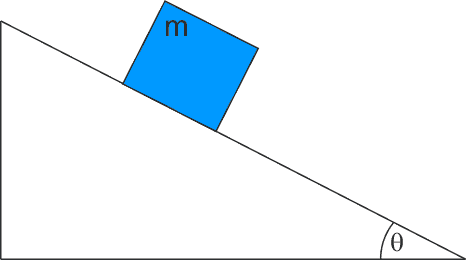
Ćwiczenie Oblicz przyspieszenie z jakim porusza się klocek o masie m zsuwający się bez tarcia po równi pochyłej o kącie nachylenia θ (tak jak na rysunku). Sprawdź obliczenia i wynik. |
Teraz możesz poznać bardziej zaawansowany przykład. Więcej o ... (Ruch w polu grawitacyjnym z uwzględnieniem oporu powietrza).


 Podstawy dynamiki, wstęp
Podstawy dynamiki, wstęp
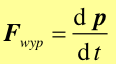 lub
lub