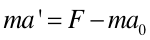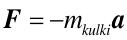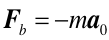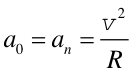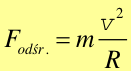5.2 Siły bezwładności
Omawiając zasady dynamiki Newtona wprowadziliśmy ważne pojęcie fizyczne:
zdefiniowaliśmy inercjalny układ odniesienia. Stwierdziliśmy wtedy, że układy inercjalne są
tak istotne bo we wszystkich takich układach ruchami ciał rządzą dokładnie
te sama prawa, i dlatego większość zagadnień staramy się
rozwiązywać właśnie w inercjalnych układach odniesienia. Nasuwa się jednak pytanie,
jak stosować zasady dynamiki Newtona w układzie odniesienia, który doznaje przyspieszenia.
Na przykład co możemy powiedzieć o siłach jakich działania "doznajemy" gdy
znajdujemy się w samochodzie, który przyspiesza, hamuje lub zakręca?
W tym celu rozpatrzymy ruch ciała o masie m poruszającego się wzdłuż osi x ruchem przyspieszonym,
pod wpływem działania siły F = ma. Ruch ten jest obserwowany z dwóch różnych układów
odniesienia (dwaj obserwatorzy), z których jeden xy jest układem
inercjalnym, a drugi x'y' porusza się względem pierwszego wzdłuż
osi x (rysunek poniżej).
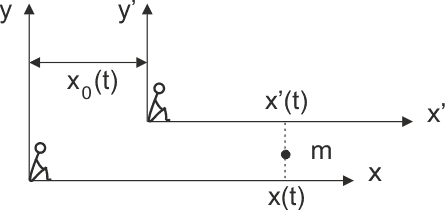
Rys. 5.2. Położenie ciała m w dwóch układach odniesienia
Odległość miedzy dwoma obserwatorami (układami) wynosi w danej chwili x0(t) więc związek między położeniem ciała rejestrowanym przez obu obserwatorów ma postać
| (5.5) |
Natomiast przyspieszenie w obu układach znajdujemy korzystając z równań (3.1)
| (5.6) |
to znaczy, różniczkując dwukrotnie równanie (5.5)
| (5.7) |
Widać, że przyspieszenia w obu układach są równe tylko wtedy gdy a0
= 0 więc gdy układ x'y' porusza się względem układu
xy ruchem jednostajnym lub względem niego spoczywa to znaczy gdy układ
x'y' też jest układem inercjalnym tak jak xy.
Natomiast gdy a0 ≠ 0 to układ
x'y' nazywamy układem nieinercjalnym
![]() ,
a jego przyspieszenie a0 przyspieszeniem
unoszenia
,
a jego przyspieszenie a0 przyspieszeniem
unoszenia ![]() .
Widzimy, że przyspieszenie ciała zależy od przyspieszenia układu
odniesienia (od przyspieszenia obserwatora), w którym jest mierzone więc
druga zasada dynamiki jest słuszna tylko, gdy obserwator znajduje się w układzie
inercjalnym. Inaczej mówiąc, prawa strona równania F = ma
zmienia się w zależności od przyspieszenia obserwatora. Jeżeli pomnóżmy
równanie (5.7) obustronnie przez m to otrzymamy
.
Widzimy, że przyspieszenie ciała zależy od przyspieszenia układu
odniesienia (od przyspieszenia obserwatora), w którym jest mierzone więc
druga zasada dynamiki jest słuszna tylko, gdy obserwator znajduje się w układzie
inercjalnym. Inaczej mówiąc, prawa strona równania F = ma
zmienia się w zależności od przyspieszenia obserwatora. Jeżeli pomnóżmy
równanie (5.7) obustronnie przez m to otrzymamy
|
(5.8) |
Widzimy, że w układzie x'y' (przyspieszającym) zasady dynamiki Newtona nie są spełnione bo:
- Gdy na ciało nie działa siła (F = 0) to ciało nie spoczywa ani nie porusza się ruchem jednostajnym prostoliniowym tylko ruchem przyspieszonym z przyspieszeniem -a0.
- Iloczyn masy i przyspieszenia nie równa się sile działającej F ale jest mniejszy od niej o iloczyn ma0.
|
Definicja Ten iloczyn masy i przyspieszenia unoszenia (ze znakiem minus) nazywamy siłą bezwładności Fb . |
Ze wzoru (5.8) wynika, że jeżeli w układach nieinercjalnych chcemy
stosować drugą zasadę dynamiki Newtona to musimy uwzględniać siły bezwładności.
Jak już mówiliśmy istnieją tylko
cztery podstawowe oddziaływania, z których wynikają wszystkie siły
zaobserwowane we Wszechświecie. Wszystkie te siły nazywamy siłami
rzeczywistymi, ponieważ możemy je zawsze związać z działaniem
pochodzącym od konkretnym ciał materialnych. Inaczej jest z siłami bezwładności,
które nie pochodzą od innych ciał, a ich obserwowanie jest związane wyłącznie
z wyborem nieinercjalnego układu odniesienia. Dlatego siły bezwładności
nazywamy siłami pozornymi ![]() .
.
Przykład
Dwaj obserwatorzy opisują ruch kulki w sytuacji pokazanej na rysunku poniżej.
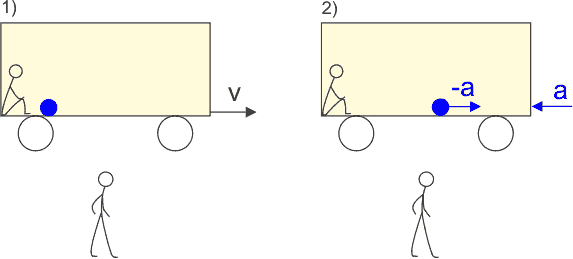
Rys. 5.3. Ruch kulki obserwowany z różnych układów odniesienia
Jeden z obserwatorów znajduje się w samochodzie, a drugi stoi na Ziemi.
Samochód początkowo porusza się ze stałą prędkością v
po linii prostej (rys. 1), następnie hamuje ze stałym opóźnieniem a
(rys. 2). Między kulką, a podłogą samochodu nie ma tarcia. Gdy samochód
jedzie ze stałą prędkością to obydwaj obserwatorzy stwierdzają
zgodnie, na podstawie pierwszej zasady dynamiki, że na kulkę nie działa
żadna siła: obserwator w samochodzie zauważa, że
vkulki = 0 → F = 0, a
obserwator stojący obok stwierdza, że vkulki = v
= const. → F = 0. Zwróćmy uwagę, że obserwatorzy znajdują się w inercjalnych
układach odniesienia.
Sytuacja zmienia się gdy samochód zaczyna hamować (rys. 2).
Obserwator związany z Ziemią dalej twierdzi, że kulka porusza się ze stałą
prędkością, a tylko podłoga samochodu przesuwa się pod nią, bo
samochód hamuje. Natomiast obserwator w samochodzie stwierdza, że kulka
zaczyna się poruszać się z przyspieszeniem –a w stronę
przedniej ściany wózka. Dochodzi do wniosku, że na kulkę o masie mkulki
zaczęła działać siła
| (5.9) |
ale nie może wskazać żadnego ciała, będącego źródłem tej siły. Mówiliśmy już, że druga zasada dynamiki jest słuszna tylko w
inercjalnym układzie odniesienia. Zauważmy, że obserwator w wózku znajduje się teraz w układzie nieinercjalnym i siła jakiej działanie
zauważa jest pozorną siłą bezwładności ![]() .
.
Działanie sił bezwładności odczuwamy nie tylko podczas przyspieszania i hamowania (przyspieszenie styczne), ale również gdy zmienia się kierunek prędkości. Zgodnie z definicją siły bezwładności
| (5.10) |
a dla ruchu krzywoliniowego przyspieszenie układu jest przyspieszeniem normalnym (dośrodkowym w ruchu po okręgu)
| (5.11) |
więc wartość siły bezwładności wynosi
| (5.12) |
Tę siłę bezwładności nazywamy siłą odśrodkową
![]() .
Z taką siłą mamy do czynienia na przykład podczas jazdy samochodem na zakręcie. Również Ziemia nie jest idealnym układem
inercjalnym ponieważ wiruje. Jednak w większości rozpatrywanych
przez nas zjawisk można zaniedbać wpływ ruchu Ziemi na ich przebieg.
.
Z taką siłą mamy do czynienia na przykład podczas jazdy samochodem na zakręcie. Również Ziemia nie jest idealnym układem
inercjalnym ponieważ wiruje. Jednak w większości rozpatrywanych
przez nas zjawisk można zaniedbać wpływ ruchu Ziemi na ich przebieg.
Tu dowiesz się Więcej o ... siłach bezwładności (siła Coriolisa).
Na zakończenie spróbuj rozwiązać następujący problem
|
Ćwiczenie Winda rusza w dół i przez pewien czas porusza się ruchem jednostajnie przyspieszonym. Czas t spadania ciała puszczonego swobodnie w tej windzie, na drodze od sufitu do podłogi, jest o 25% większy niż niż czas t0 w windzie stojącej. Oblicz przyspieszenie windy. Dane jest przyspieszenie ziemskie g. Sprawdź obliczenia i wynik. |


 Siły kontaktowe i tarcie
Siły kontaktowe i tarcie
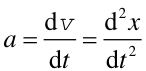
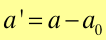
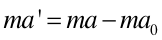 lub
lub