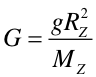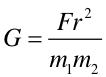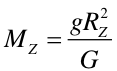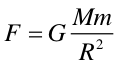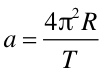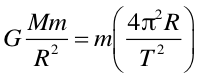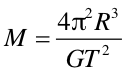6.1 Prawo powszechnego ciążenia
Przedstawimy, teraz jedno z czterech podstawowych oddziaływań - oddziaływanie grawitacyjne.
Rozważania dotyczące grawitacji rozpoczniemy od prostego przykładu.
Przykład
Obliczmy stosunek przyspieszenia dośrodkowego Księżyca w kierunku
Ziemi do przyspieszenia grawitacyjnego przy powierzchni Ziemi.
Przyspieszenie dośrodkowe w ruchu jednostajnym po okręgu możemy
obliczyć na podstawie równania (3.16)
|
gdzie RK = 3.86·105 km jest odległością od Ziemi do Księżyca. Okres obiegu Księżyca wokół Ziemi wynosi T = 27.3 dnia. Otrzymujemy więc aK = 2.73·10-3 m/s2. Natomiast w pobliżu powierzchni Ziemi przyspieszenie wynosi 9.8 m/s2.
Stosunek tych przyspieszeń
|
Ponieważ promień Ziemi wynosi RZ = 6300 km to zauważmy, że w granicach błędu
|
(6.1) |
Newton wykonał takie obliczenia i wyciągnął wniosek, że siła przyciągania między dwoma masami (między ich środkami) maleje odwrotnie proporcjonalnie do kwadratu odległości między nimi. Ponadto zauważył, że skoro istnieje siła przyciągania pomiędzy dowolnym ciałem i Ziemią, to musi istnieć siła przyciągania między każdymi dwoma masami m1 i m2. Na tej podstawie i w oparciu o liczne obserwacje astronomiczne dokonane przez jego poprzedników min. Kopernika, Galileusza, Keplera, Newton sformułował w 1687 r prawo powszechnego ciążenia.
|
Prawo, zasada, twierdzenie Każde dwa ciała o masach m1 i m2 przyciągają się wzajemnie siłą grawitacji wprost proporcjonalną do iloczynu ich mas, a odwrotnie proporcjonalną do kwadratu odległości między nimi. |
|
(6.2) |
To jest prawo powszechne, ponieważ stosuje się do wszystkich sił grawitacyjnych; np. wyjaśnia spadanie ciał na Ziemię, ale też tłumaczy ruch planet.
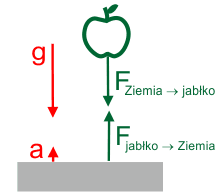
Siła z jaką Ziemia przyciąga jabłko jest taka sama co do wartości jak siła z jaką jabłko przyciąga Ziemię. Pod wpływem tej siły jabłko przyspiesza w kierunku Ziemi (z przyspieszeniem g) i Ziemia przyspiesza w kierunku jabłka (z przyspieszeniem a)
Ponieważ masa Ziemi jest tak wielka (w porównaniu z masą jabłka) przyspieszenie a jest niemierzalnie małe i mówimy, że jabłko spada na Ziemię. |
Rys. 6.1. Oddziaływanie grawitacyjne Ziemia - jabłko. |
Wartość współczynnika proporcjonalności G, nazywanego stałą grawitacji, Newton oszacował stosując równanie (6.2) do siły działającej między Ziemią, a ciałem o masie m. Zgodnie z zasadą dynamiki
|
|
|
(6.3) |
gdzie RZ jest promieniem Ziemi. Masę Ziemi MZ Newton obliczył zakładając średnią gęstość Ziemi równą ρZ = 5·103 kg/m3 Dla porównania gęstość żelaza, głównego składnika masy Ziemi, wynosi ρFe = 7.9·103·kg/m3, a gęstość krzemu, podstawowego składnika skorupy ziemskiej, wynosi ρSi = 2.8·103 kg/m3.
Uwzględniając RZ = 6.37·106 m Newton otrzymał wartość G = 7.35·10-11 Nm2/kg2 co jest wartością tylko o 10% większą niż ogólnie dzisiaj przyjmowana wartość 6.67·10-11 Nm2/kg2. Wartość stałej G obliczonej przez Newtona jest obarczona błędem wynikającym z przyjętej średniej wartości gęstości Ziemi.
Żeby wyznaczyć stałą G w laboratorium niezależnie od masy Ziemi i tym samym uniknąć błędu związanego z szacowaniem gęstości Ziemi trzeba by zmierzyć siłę oddziaływania dwóch mas m1 i m2 umieszczonych w odległości r. Wówczas
|
Zauważmy jednak, że przykładowo dla mas każda po 1 kg oddalonych od siebie o 10 cm siła F ma wartość F = 6.67·10-9 N i jest za mała by ją dokładnie zmierzyć standardowymi metodami. Problem pomiaru tak małej siły rozwiązał Cavendish.
Doświadczenie Cavendisha
W swoim pomiarze Cavendish wykorzystał fakt, że siła potrzebna do skręcenia długiego, cienkiego włókna kwarcowego jest bardzo mała. Na takim włóknie zawiesił pręt z dwiema małymi kulkami ołowianymi (m) na końcach (rysunek poniżej). Następnie w pobliżu każdej z kulek umieścił większą kulę ołowianą (M) i zmierzył precyzyjnie kąt α o jaki obrócił się pręt.
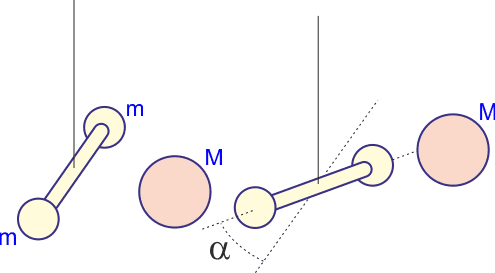
Pomiar wykonany metodą Cavendisha dał wartość G = 6.67·10-11 Nm2/kg2. Znając już wartość stałej G, Cavendish wyznaczył masę Ziemi MZ z równania
|
(6.4) |
Cavendish wyznaczył też masę Słońca i masy planet, tych których satelity zostały zaobserwowane.
Przykład
Rozpatrzmy ruch planety o masie m krążącej w odległości R wokół Słońca o masie M. Wtedy siła przyciągania grawitacyjnego wynosi
|
(6.5) |
a ponieważ przyspieszenie w ruchu po okręgu jest dane wyrażeniem
|
(6.6) |
to równanie (6.5) przyjmuje postać
|
(6.7) |
skąd otrzymujemy
|
(6.8) |
|
Ćwiczenie Oblicz jaki był okres obiegu Księżyca przez moduł statku Apollo? Dane są: promień Księżyca RK = 1740 km, jego masa MK = 7.35·1022 kg oraz stała G = 6.67·10−11 Nm2/kg2. Sprawdź obliczenia i wynik. |
|
Ćwiczenie Korzystając z tego wyrażenia oblicz masę Słońca przyjmując odległość Ziemia – Słońce równą R = 1.5·108 km, oraz okres obiegu T = 1 rok. Porównaj ten wynik z masą Ziemi obliczoną na podstawie równania (6.4). Ile razy masa Słońca jest większa od masy Ziemi? Sprawdź obliczenia i wynik. |


 Siły bezwładności
Siły bezwładności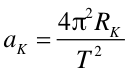
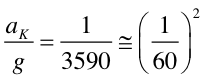
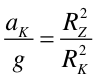

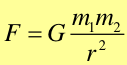
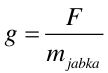
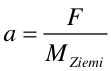
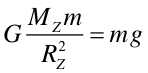 skąd
skąd