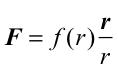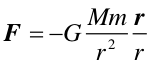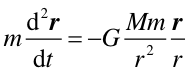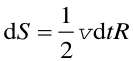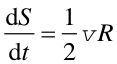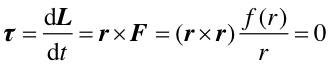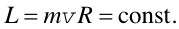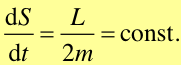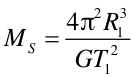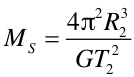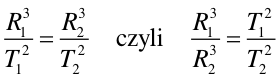Prawa Keplera a zasady dynamiki Newtona

Pierwsze prawo Keplera wynika z tego, że siła grawitacyjna jest siłą centralną, tj. taką, która zawsze skierowana jest do określonego punktu - centrum siły. Jeżeli początek układu współrzędnych umieścimy w centrum siły, to siłę centralną można zapisać ogólnie w postaci

(1)

lub dla siły grawitacji

(2)

Równanie opisujące ruch pod wpływem siły grawitacji ma więc postać

(3)

Rozwiązaniem tego równania są krzywe stożkowe tj. krzywe będące przekrojami stożka, takie jak elipsa, parabola, hiperbola (rysunek poniżej).

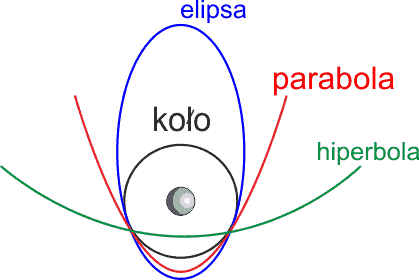
Rys. 1. Krzywe stożkowe – tor ruchu w polu siły grawitacji

Teraz przejdziemy do drugiego prawa Keplera. Na rysunku 2 zaznaczona jest powierzchnia zakreślana w czasie Δt przez linię łączącą planetę ze Słońcem.

Rys. 2. Powierzchnia zakreślana w czasie Δt przez linię łączącą planetę ze Słońcem

Jeżeli weźmiemy bardzo krótki przedział czasu dt (Δt → 0) to zaznaczone pole dS jest powierzchnią trójkąta o podstawie równej długości zakreślanego łuku (vdt) i wysokości równej promieniowi R

(4)

Z równania (4) wynika, że chwilowa prędkość polowa (prędkość z jaką promień R zakreśla powierzchnię) jest równa

(5)

Z definicji siły centralnej (1) wynika że moment siły τ dla siły centralnej jest równy zeru

(6)

z czego wynika, że moment pędu L jest zachowany w ruchu pod wpływem siły centralnej np. w ruchu planety w jej obiegu wokół Słońca (zasadę zachowania momentu pędu poznamy w następnych rozdziałach).

(7)

Łącząc równania (5) i (7) otrzymujemy ostatecznie

(8)

Na koniec rozpatrzymy trzecie prawo Keplera dla planet poruszających się po orbitach kołowych. Korzystając z otrzymanego uprzednio wzoru (6.8) na masę Słońca otrzymujemy dla pierwszej planety krążącej wokół Słońca

	(9)
a dla drugiej

(10)

Porównując te równania stronami otrzymujemy

(11)

Równanie (11) wyraża drugie prawo Keplera.