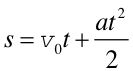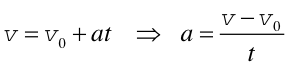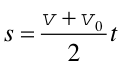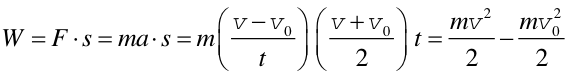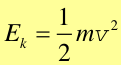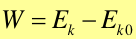Praca wykonana przez siłę zmienną7.3 Energia kinetyczna
Rozpatrzmy jeszcze raz ruch ciała pod wpływem stałej, niezrównoważonej siły F i obliczmy pracę jaką wykonuje ona na drodze s. Stałość siły oznacza, że ruch odbywa się ze stałym przyspieszeniem a. Zakładamy ponadto, że kierunek siły F i przyspieszenia a pokrywa się z kierunkiem przesunięcia s. Dla ruchu jednostajnie przyspieszonego możemy napisać
|
(7.6a) |
|
(7.6a) |
co w połączeniu daje
|
(7.7) |
Wykonana praca jest równa
|
(7.8) |
|
Definicja Połowę iloczynu masy ciała i kwadratu prędkości nazywamy energią kinetyczną Ek ciała o masie m. |
|
(7.9) |
Na podstawie wzorów (7.8) i (7.9) widzimy, że
|
Prawo, zasada, twierdzenie Praca wykonana przez siłę F działającą na ciało o masie m jest równa zmianie energii kinetycznej tego ciała. |
|
(7.10) |
To jest twierdzenie o pracy i energii.
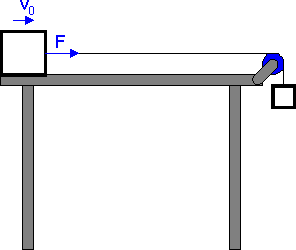
Przykład jest pokazany na rysunku poniżej (animacja). Stała siła F z jaką ciągnięty jest po gładkim stole klocek wykonuje pracę W i dzięki temu rośnie energia kinetyczna klocka (zwróć uwagę, że rośnie jego prędkość v).
Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.
Rys. 7.5. Przykład ilustrujący twierdzenie o pracy i energii
Z twierdzenia o pracy i energii wynika, że jednostki pracy i energii są takie same.
|
Jednostki Jednostką pracy i energii jest w układzie SI dżul (J); 1J = 1N·m. W fizyce atomowej powszechnie używa się jednostki elektronowolt (eV); 1eV = 1.6·10-19 J. |
Spróbuj teraz wykonać proste ćwiczenie.
|
Ćwiczenie Porównaj energię kinetyczną sprintera o masie 80 kg biegnącego z prędkością 10 m/s z energią kinetyczną pocisku o masie 5 g wylatującego z karabinu z prędkością 800 m/s. Pamiętaj, żeby podać wynik w odpowiednich jednostkach. |
