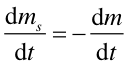Układy o zmiennej masie

Rozpatrzymy układ, który stanowi rakieta wyrzucająca ze swej dyszy gorący gaz z dużą prędkością, zmniejszając w ten sposób swoją masę i zwiększając prędkość (rysunek poniżej).

Rys. 1. Napęd odrzutowy rakiety

Spaliny opuszczają silnik rakiety ze stałą prędkością v_s względem Ziemi. Prędkość chwilowa rakiety względem Ziemi jest równa v, zatem prędkość spalin względem rakiety v_wzg jest dana zależnością

(1)

Jeżeli w przedziale czasu dt z rakiety wyrzucona zostaje masa dm_s z prędkością v_s to masa rakiety maleje o dm, a jej prędkość rośnie o dv, przy czym

(2)

Znak minus wynika stąd, że masa rakiety maleje. Obliczamy teraz zmianę pędu P układu w czasie dt

(3)

lub

(4)

skąd ostatecznie

(5)

Równanie to uwzględnia fakt, że w przypadku rakiety zmienia się zarówno jej masa jak i prędkość podczas gdy spaliny są wyrzucane ze stałą prędkością.
Zmiana pędu układu jest zgodnie z drugą zasadą dynamiki Newtona równa sile zewnętrznej działającej na układ. Uwzględniając zależności (1) i (2) możemy przekształcić równanie (5) do postaci

(6)

Ostatni wyraz w równaniu (6) może być interpretowany jako siła wywierana na układ przez substancję (spaliny), która z niego wylatuje. W przypadku rakiety (samolotu) nosi ona nazwę siły ciągu .

Przykład

Samolot odrzutowy leci z prędkością 250 m/s i z taką prędkością jest wciągane do jego silnika powietrze. W każdej sekundzie silnik samolotu spala mieszankę paliwową składającą się z 75 kg powietrza i 3 kg paliwa, a prędkość wyrzucania spalin wynosi 500 m/s.
Siłę ciągu obliczamy zgodnie ze wzorem (6) przy czym prędkość względna jest równa różnicy prędkości wyrzucania spalin i wciągania powietrza
v_wzg = 250 m/s, a masa spalin wyrzucanych w jednostce czasu wynosi 78 kg/s. Stąd otrzymujemy siłę ciągu równą 1.95·10⁴ N.

Jeżeli ruch rakiety odbywa się w przestrzeni kosmicznej to siły zewnętrzne F_zew są do zaniedbania i wtedy zmiana pędu rakiety jest równa sile ciągu (jest spełniona zasada zachowania pędu). Natomiast gdy ruch odbywa się w pobliżu Ziemi (np. tuż po starcie) to wówczas F_zew reprezentuje ciężar rakiety i siłę oporu atmosfery i trzeba ją uwzględnić. Konstruktorzy rakiet starają się uzyskać jak największą siłę ciągu aby przezwyciężyć F_zew. Np. rakieta Saturn 5, o masie ponad 3000 ton, wytwarzała przy starcie siłę ciągu 40 MN.