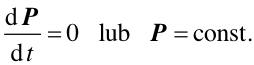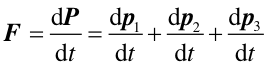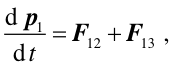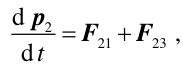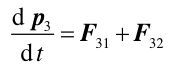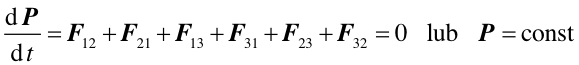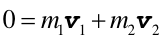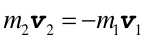9. Zasada zachowania pędu
• Spis treści  
• Zderzenia w przestrzeni 1-wymiarowej  
•   Pęd układu punktów materialnych

9.4 Zasada zachowania pędu

  Ponownie rozpatrzmy układ n punktów materialnych. Jeżeli układ jest odosobniony, to znaczy nie działają siły zewnętrzne to zgodnie z równaniem (9.14)

Ten warunek wyraża zasadę zachowania pędu.

Ta sytuacja jest zilustrowana na rysunku poniżej przykładowo dla układu trzech oddziaływujących mas (punktów materialnych).

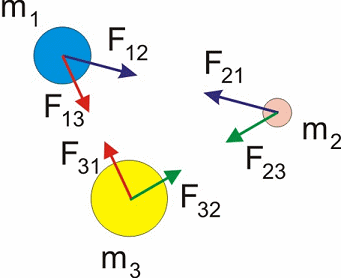
 Rys. 9.3. Układ trzech oddziaływujących mas

Druga zasada dynamiki Newtona dla tego układu punktów materialnych przyjmuje postać

jeżeli nie działają siły zewnętrzne.

Zobaczymy teraz jak ta zasada stosuje się do wybranej sytuacji.

Przykład

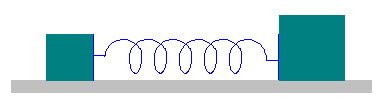
Rozważmy dwa ciała o masach m₁ i m₂ połączone nieważką sprężyną umieszczone na doskonale gładkim stole. Odciągamy od siebie te ciała na pewną odległość, a następnie puszczamy swobodnie. Ruch tych ciał pokazany jest na rysunku-animacji poniżej.

Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.

 Rys. 9.4. Układ dwóch mas połączonych sprężyną

Spróbujmy opisać ruch tych ciał.
Jeżeli pod pojęciem układ rozumiemy obie masy i sprężynę to na ten układ nie działa żadna siła zewnętrzna (układ odosobniony), działają tylko siły pomiędzy elementami układu. Oznacza to, że możemy do tego układu stosować zasadę zachowania pędu. Przed zwolnieniem ciał pęd układu (w odniesieniu do stołu) był równy zeru. Pęd zostaje zachowany więc pozostaje taki sam po zwolnieniu obu ciał. Chociaż poszczególne ciała poruszają się i ich pędy są różne od zera to pęd układu może być równy zeru. Pęd układu będący wielkością wektorową jest sumą dodatniego pędu ciała m₁ (porusza się w kierunku +x) i ujemnego pędu ciała m₂ (porusza się w kierunku −x). Pęd nieważkiej sprężyny jest równy zeru. Z zasady zachowania pędu wynika, że pęd początkowy układu jest równy pędowi w dowolnej chwili co możemy zapisać w postaci równania

Przykładowo gdy m₁ = 1 kg i m₂ = 2 kg to v₁ jest dwukrotnie większa od v₂ i ma zwrot przeciwny.

Analogicznie posługując się zasadą zachowania pędu można wytłumaczyć zjawisko odrzutu występujące przy strzelaniu z broni palnej.
Zjawisko odrzutu ma jednak ważne praktyczne znaczenie. Zostało wykorzystane w silnikach odrzutowych i rakietowych, w których wyrzucane spaliny nadają samolotowi (rakiecie) przeciwnie skierowany pęd. Zjawisko to jednak różni się od opisanych powyżej, bo w przeciwieństwie do układów gdzie masa elementów składowych pozostawała stała masa wyrzucanych spalin i masa rakiety zmieniają się  Więcej o ... .

Wiemy już, że jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru to spełniona jest zasada zachowania pędu. W takim układzie mogą jednak działać siły wewnętrzne, na przykład siły występujące przy zderzeniach między cząsteczkami gazu. I właśnie dlatego możemy skorzystać z zasady zachowania pędu do opisu zderzeń.