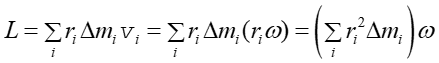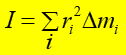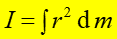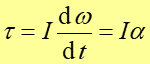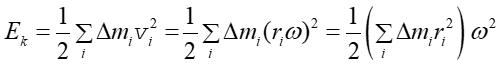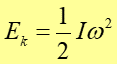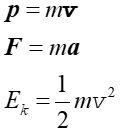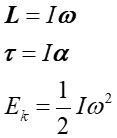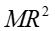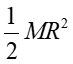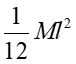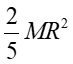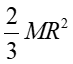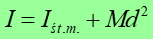11.3 Dynamika bryły sztywnej
Większość ciał w przyrodzie to nie punkty materialne ale rozciągłe ciała sztywne. Przeanalizujmy teraz ruch takiej bryły sztywnej obracającej się ze stałą prędkością kątową ω wokół stałej osi obrotu w układzie środka masy. Zauważmy, że chociaż wszystkie punkty mają te samą prędkość kątową ω to punkty znajdujące się w różnych odległościach od osi obrotu mają różną prędkość liniową v (rysunek 11.3). Prędkość i -tego punktu o masie Δmi wynosi vi = ri ω gdzie ri jest odległością od osi obrotu
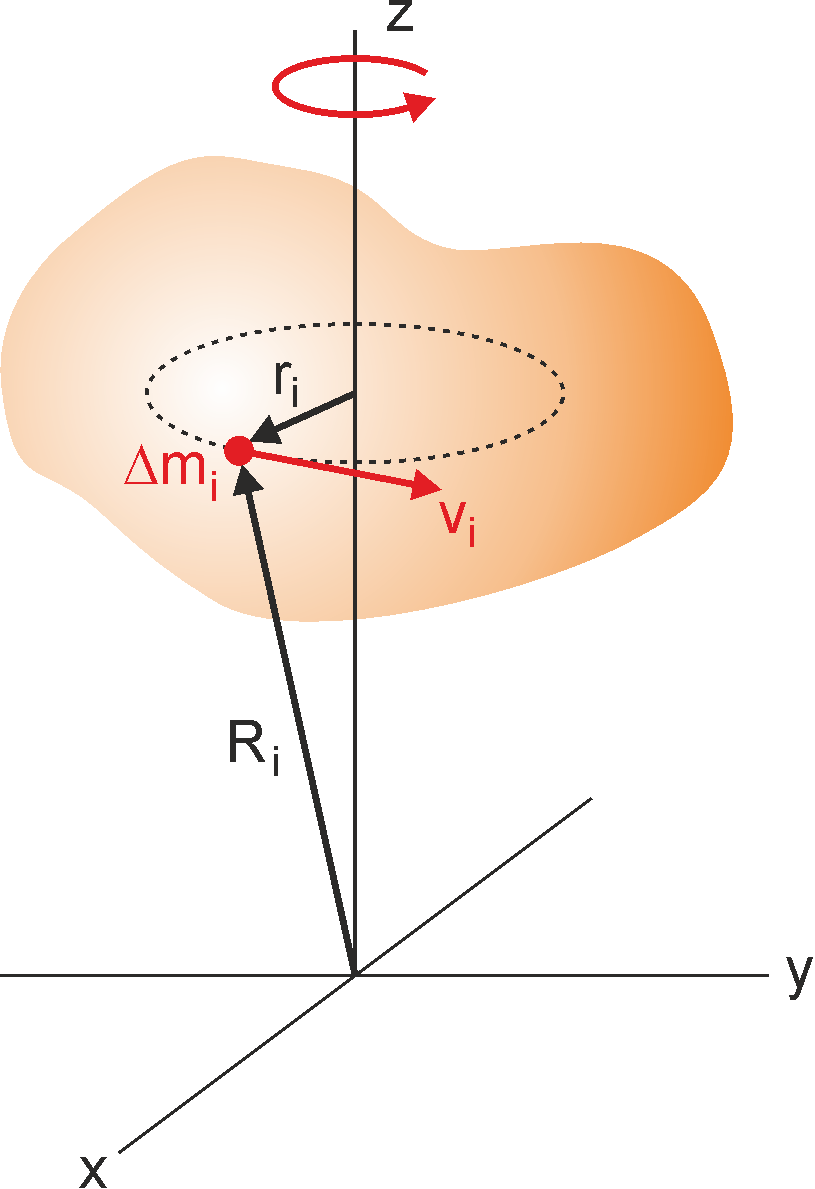
Rys. 11.3. Obracająca się bryła sztywna
Obliczamy teraz wartość momentu pędu L tego ciała
|
(11.13) |
Wielkość w nawiasie nazywamy momentem bezwładności
I ![]() , który definiujemy jako
, który definiujemy jako
|
Definicja |
|
(11.14) |
a dla ciągłego rozkładu masy
|
Definicja |
|
(11.15) |
Zwróćmy uwagę, że moment bezwładności I zależy od osi obrotu. Możemy teraz wyrazić moment pędu poprzez moment bezwładności
|
(11.16) |
a ponieważ zgodnie z równaniem (11.10) 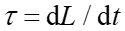 więc
więc
|
(11.17) |
gdzie α jest przyspieszeniem kątowym. Obliczmy teraz energię kinetyczną obracającego się ciała
|
(11.18) |
|
(11.19) |
Zestawmy teraz odpowiednie wielkości obliczone dla ruchu obrotowego z ich odpowiednikami dla ruchu postępowego.
Tab. 11.2. Porównanie ruchu postępowego i obrotowego
| Ruch postępowy | Ruch obrotowy |
|---|---|
|
|
Z tego porównania widać, że moment bezwładności I jest analogiczną wielkością do masy m w ruchu postępowym. Zwróćmy uwagę, że w przeciwieństwie do masy moment bezwładności zależy od osi, wokół której obraca się ciało. Momenty bezwładności niektórych ciał sztywnych są podane w tabeli 11.3.
Tab. 11.3. Momenty bezwładności wybranych ciał sztywnych
| Obiekt | Moment bezwładności I |
|---|---|
| Obręcz, pierścień o promieniu R, względem osi obręczy |
|
| Krążek, walec względem osi walca |
|
| Pręt o długości d, względem osi symetrii prostopadłej do pręta |
|
| Pełna kula o promieniu R, względem średnicy |
|
| Czasza kulista o promieniu R, względem średnicy |
|
Więcej o ... obliczaniu momentów bezwładności.
Często do obliczania momentu bezwładności wygodnie jest posłużyć się twierdzeniem Steinera. Podaje ono zależność pomiędzy momentem bezwładności I ciała względem danej osi, a momentem bezwładności Iśr.m. tego ciała względem osi przechodzącej przez jego środek masy i równoległej do danej. Związek ten wyraża się zależnością
|
Prawo, zasada, twierdzenie |
|
(11.20) |
gdzie a jest odległością między osiami, a M jest masą ciała.
|
Ćwiczenie Teraz korzystając z powyższego twierdzenia i z danych w tabeli 11.3 oblicz moment bezwładności pręta o masie M i długości d względem osi prostopadłej do pręta i przechodzącej przez jeden z jego końców. Sprawdź obliczenia i wynik. |


 Dynamika ruchu obrotowego
Dynamika ruchu obrotowego