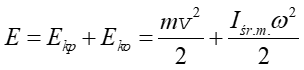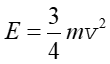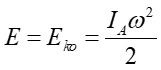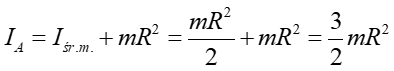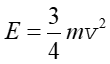Ruch obrotowo-postępowy

11.4 Ruch obrotowo-postępowy

Na co dzień często mamy do czynienia z toczeniem się ciał. W przeciwieństwie do ruch obrotowego względem nieruchomej osi obrotu w przypadku toczenia występuje zarówno ruch postępowy, jak i obrotowy. Dlatego spróbujemy opisać toczenie jako złożenie ruchu postępowego i obrotowego. W tym celu prześledźmy ruch walca o promieniu R pokazany na rysunku 11.4.

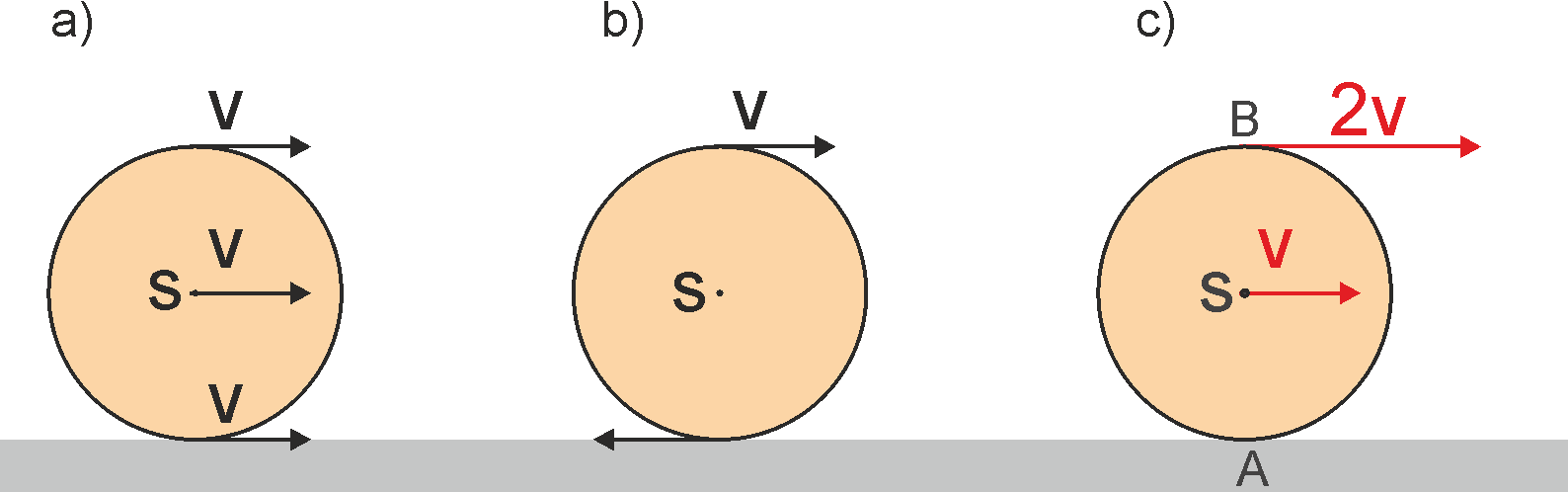
Rys. 11.4. Toczenie (c) jako złożenie ruchu postępowego (a) i obrotowego (b)

W ruchu postępowym, rysunek (a), wszystkie punkty poruszają się z takimi samymi prędkościami, natomiast w ruchu obrotowym wokół środka masy S, rysunek (b), przeciwległe punkty poruszają się z przeciwnymi prędkościami, a środek jest nieruchomy. Na rysunku (c) pokazano wynik złożenia (sumowania) odpowiednich wektorów z rysunków (a) i (b). Zwróćmy uwagę, że podstawa walca (punkt A styczności z podłożem) w każdej chwili spoczywa (prędkość chwilowa v_A = 0). Natomiast prędkość liniowa punktów S i B jest proporcjonalna do ich odległości od punktu A (punkt B w odległości 2R ma prędkość dwukrotnie większą niż punkt S w odległości R). Jeszcze pełniej widać to na rysunku 11.6 gdzie narysowane są prędkości chwilowe kilku punktów na obwodzie toczącego się walca.

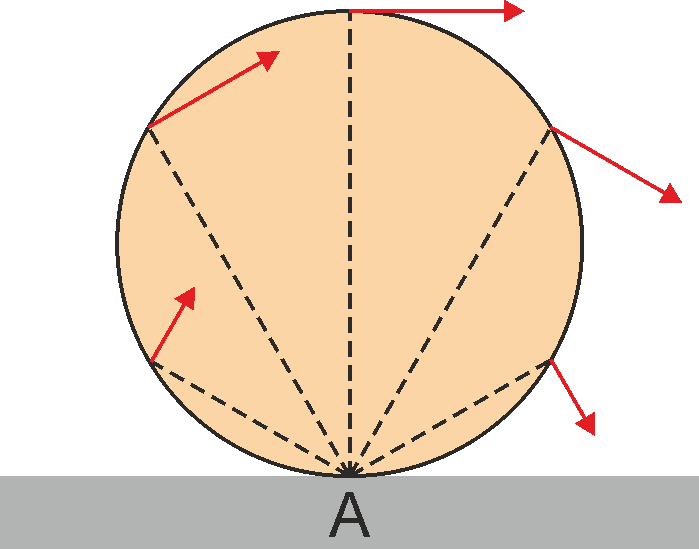
Rys. 11.5. Toczenie się walca jako obrót wokół punktu A

Widać, że prędkość każdego z tych punktów jest prostopadła do linii łączącej ten punkt z podstawą A i proporcjonalna do odległości tego punktu od A. Takie zachowanie jest charakterystyczne dla ciała wykonującego ruch obrotowy względem nieruchomej osi. Oznacza to, że opisywany walec obraca się wokół punktu A, a co za tym idzie, że możemy toczenie opisywać również wyłącznie jako ruch obrotowy ale względem osi przechodzącej przez punkt A styczności z powierzchnią, po której toczy się ciało.
W celu zilustrowania równoważności obu opisów obliczymy teraz energię kinetyczną walca o masie m toczącego się z prędkością v. Najpierw potraktujemy toczenie jako złożenie ruchu postępowego i obrotowego względem środka masy. Energię kinetyczną obliczamy jako sumę energii ruchu postępowego i obrotowego

(11.21)

Podstawiając wartość momentu bezwładności walca odczytaną z tabeli 11.3 oraz uwzględniając, że dla ciała toczącego się bez poślizgu ω = v/R (równanie 11.1) otrzymujemy

(11.22)

Teraz powtórzymy nasze obliczenia ale potraktujemy toczenie wyłącznie jako obrót względem osi obrotu w punkcie A zetknięcia walca z powierzchnią. Energia kinetyczną obliczamy więc jako

(11.23)

Moment bezwładności walca I_A ,względem osi A, obliczamy z twierdzenia Steinera

(11.24)

Po podstawieniu tej wartości i uwzględniając, że ω = v/R (równanie 11.1) otrzymujemy

(11.25)

W obu przypadkach otrzymaliśmy ten sam rezultat. Widzimy, że

Prawo, zasada, twierdzenie
Ruch ciała będący złożeniem ruchu postępowego środka masy i obrotowego względem osi przechodzącej przez środek masy jest równoważny ruchowi obrotowemu wokół osi przechodzącej przez punkt styczności ciała z powierzchnią, po której się ono toczy.

Ćwiczenie
Krążek (walec) i kula o takich samych masach m i promieniach R staczają się bez poślizgu po równi pochyłej z wysokości h. Korzystając z zasady zachowania energii oblicz ich prędkości u dołu równi. Jaki byłby wynik obliczeń gdyby te ciała ześlizgiwały się z równi? Obliczenia przeprowadź traktując toczenie jako złożenie ruchu postępowego i obrotowego lub jako wyłącznie jako ruch obrotowy. Sprawdź obliczenia i wynik.

Inny przykładem ruchu obrotowego, w którym oś obrotu nie jest nieruchomą w inercjalnym układzie odniesienia jest bąk wirujący dookoła pewnej osi symetrii. Więcej o ...