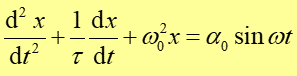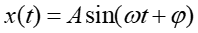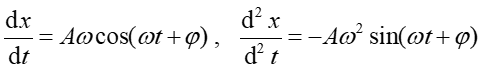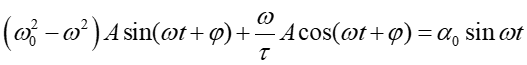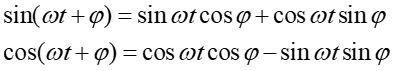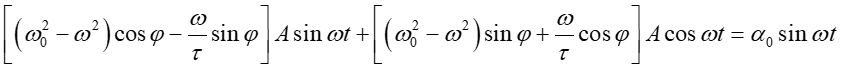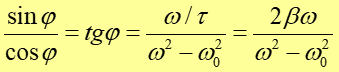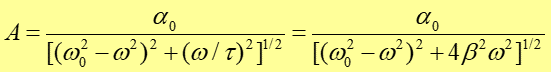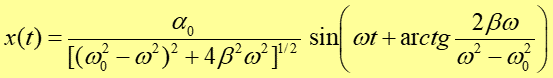Amplituda i faza w ruchu harmonicznym wymuszonym
Szukamy rozwiązania równania różniczkowego
|
(1) |
w postaci
|
(2) |
W tym celu obliczamy odpowiednie pochodne funkcji (2)
|
(3) |
i podstawiamy do równania (1), które przyjmuje postać
|
(4) |
Równanie to przekształcamy korzystając ze związków
|
Otrzymujemy równanie
|
(5) |
Powyższa równość może być spełnione tylko, gdy czynniki stojące przy przy funkcji sin;ωt i cosωt po obu stronach równania będą sobie równe. Ten warunek oznacza, że czynnik przy cosωt ma być równy zeru co można zapisać jako
|
(5) |
Z tego warunku znamy już φ. Teraz możemy wyznaczyć amplitudę podstawiając odpowiednie wyrażenia za cosφ i sinφ
|
(6) |
Łącząc powyższe równania otrzymujemy
|
(7) |


 Drgania wymuszone oscylatora harmonicznego
Drgania wymuszone oscylatora harmonicznego