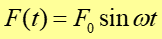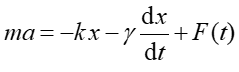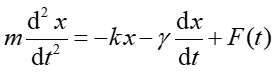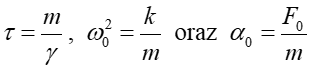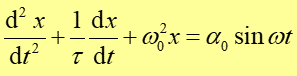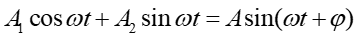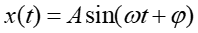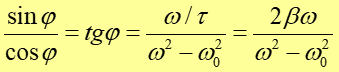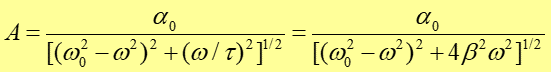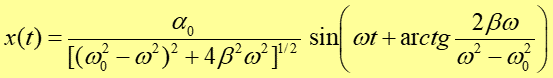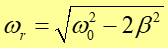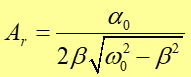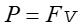12. Ruch drgający
• Spis treści  
• Składanie drgań harmonicznych  
•   Oscylator harmoniczny tłumiony

12.5 Drgania wymuszone oscylatora harmonicznego

   W ruchu harmonicznym tłumionym amplituda, a co za tym idzie i energia drgań maleje z czasem do zera. Jeżeli chcemy podtrzymać drgania to musimy działać odpowiednią siłą zewnętrzną F(t) przyłożoną do oscylatora. Siłę taką nazywamy siłą wymuszającą. W przypadku drgań harmonicznych zewnętrzna siła wymuszająca jest siłą okresowo zmienną postaci

Zwróćmy uwagę na to, że siła wymuszająca działa przez cały czas i nie należy jej mylić z krótkotrwałymi impulsami takimi jakie na przykład stosujemy gdy chcemy podtrzymać wahania huśtawki popychając ją raz na jakiś czas. Jeżeli uwzględnimy siłę wymuszającą to zgodnie z drugą zasadą dynamiki

lub korzystając z równań (3.1)

Po podstawieniu wyrażenia na siłę wymuszającą (12.34) i wprowadzeniu nowych stałych

otrzymujemy równanie analogiczne do równania (12.30) dla ruchu tłumionego

Ponownie ω₀ jest częstością własną układu, to jest częstością drgań swobodnych gdy nie działa siła zewnętrzna i nie ma tarcia ani innych sił oporu, a τ stałą czasową związaną ze współczynnikiem tłumienia β relacją 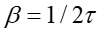. Zauważmy ponadto, że układ jest zasilany z częstością ω różną od częstości własnej ω₀.

W równaniu (12.38) mamy dwie wielkości okresowo zmienne: położenie x(t) oraz siłę wymuszającą F(t). W najogólniejszym przypadku suma (złożenie) dwóch funkcji okresowych daje w wyniku też funkcję okresową (rysunek 12.7).

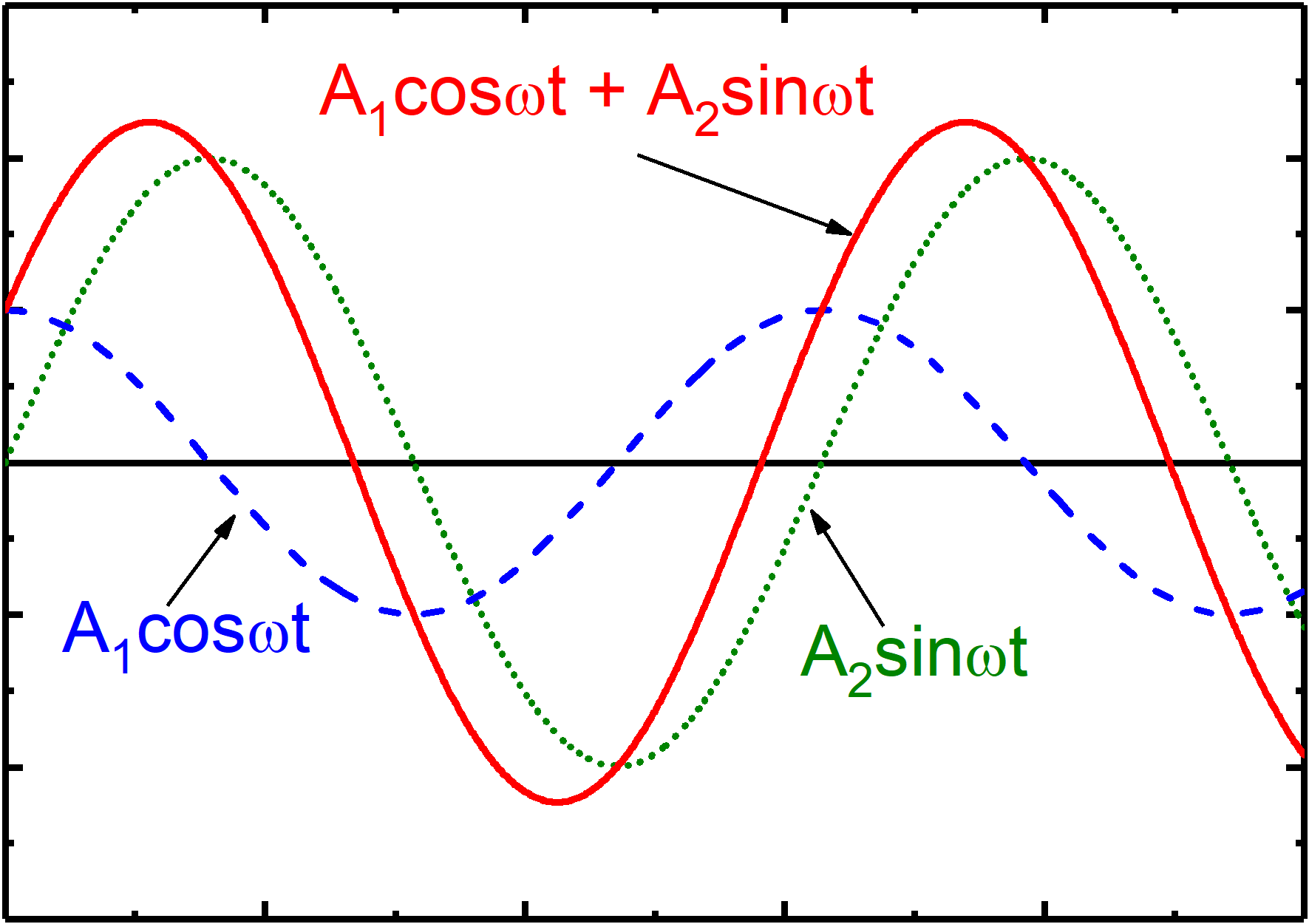
 Rys. 12.7. Złożenie dwóch funkcji okresowych

Szukamy więc rozwiązania równania (12.38) w postaci

Jak widać z porównania równania (12.34) i powyższego równania (12.40) przesunięcie fazowe φ  mówi nam o jaki kąt maksimum przemieszczenia wyprzedza maksimum siły (czyli o ile są przesunięte względem siebie funkcje sinus opisujące wychylenie (12.40) i siłę (12.34)).

Żeby znaleźć rozwiązanie musimy wyznaczyć amplitudę A oraz przesunięcie fazowe φ. W tym celu obliczamy odpowiednie pochodne funkcji (12.40) i podstawiamy do równania (12.38).  Więcej o ...  wyznaczeniu A oraz φ.
W wyniku otrzymujemy warunek na przesunięcie fazowe

i wyznaczamy amplitudę

Łącząc powyższe wzory otrzymujemy rozwiązanie

Równanie wygląda skomplikowanie ale pamiętajmy, że jest to rozwiązanie postaci .

Rezonans

Zauważmy, że chociaż drgania odbywają się z częstością ω siły wymuszającej to amplituda i faza zależą od relacji pomiędzy częstością wymuszającą ω, a częstością własną ω₀. W szczególności gdy częstość siły wymuszającej osiągnie odpowiednią częstotliwość, to amplituda drgań może wzrosnąć gwałtownie nawet przy niewielkiej wartości siły wymuszającej. To zjawisko nazywamy rezonansem . Wykres przedstawiający rezonansowy wzrost amplitudy drgań w funkcji częstości siły wymuszającej pokazany jest na rysunku 12.8 poniżej dla różnych wartości współczynnika tłumienia β.

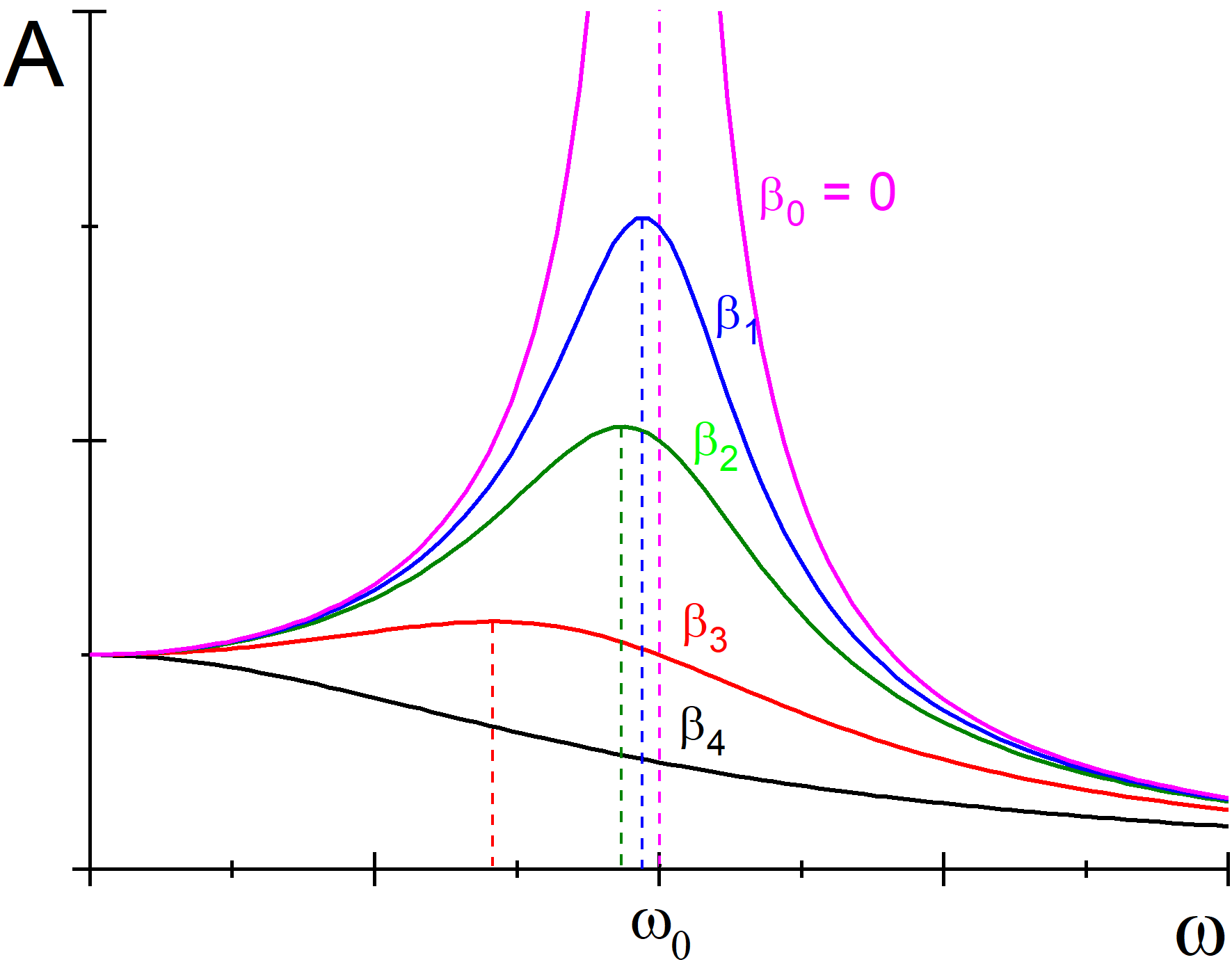
 Rys. 12.8. Krzywe rezonansu dla różnych wartości współczynnika tłumienia β (β₀ <  β₁ <  β₂ <  β₃ < β₄)

Liniami przerywanymi zaznaczono częstości rezonansowe to jest wartości częstości siły wymuszającej, dla której amplituda drgań jest maksymalna. Odpowiadająca jej amplituda nazywana jest amplitudą rezonansową . Częstość rezonansową ω_r i amplitudę rezonansową A_r możemy obliczyć z warunku na maksimum amplitudy drgań danej wzorem (12.42). Funkcja A(ω) osiąga maksimum dla częstości rezonansowej ω_r.

Podstawiając tę wartość do wzoru na amplitudę otrzymujemy wyrażenie na amplitudę rezonansową A_r

Widzimy, że dla drgań swobodnych, nietłumionych (β→0) częstość rezonansowa ω_r  jest równa częstości drgań swobodnych ω₀, a amplituda rezonansowa A_r →∞. W miarę wzrostu tłumienia wartość amplitudy rezonansowej A_r maleje, a częstość rezonansowa przesuwa się w stronę częstości mniejszych od ω₀. Dla bardzo dużego tłumienia rezonans nie występuje, maksymalna amplituda występuje dla częstości bliskiej zeru.

Dla drgań swobodnych, dla których ω_r  = ω₀ przesunięcie fazowe pomiędzy siłą, a wychyleniem, dane równaniem (12.41) jest równe φ = π/2. Oznacza to, że siła wymuszająca nie jest zgodna w fazie z wychyleniem. Zauważmy jednak, że moc pochłaniana przez oscylator zasilany siłą wymuszającą F zależy od prędkości

Warunek uzyskania rezonansu odpowiada maksimum mocy pochłanianej przez oscylator. Trzeba więc, zgodnie z powyższym wzorem, żeby to prędkość (a nie wychylenie) była zgodna w fazie z siłą, a to oznacza, że siła musi wyprzedzać wychylenie o π/2.  Więcej o ...  mocy absorbowanej przez oscylator.

Skutki rezonansu mogą być zarówno pozytywne jak i negatywne. Z jednej strony staramy się wyeliminować przenoszenie drgań na przykład z silnika na elementy nadwozia w samochodzie, a z drugiej strony działanie odbiorników radiowych i telewizyjnych jest możliwe dzięki wykorzystaniu rezonansu elektrycznego. Dostrajając odbiornik do częstości nadajnika spełniamy właśnie warunek rezonansu. Zjawisko rezonansu jest bardzo rozpowszechnione w przyrodzie.