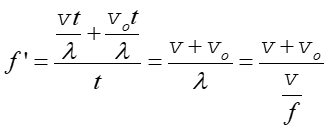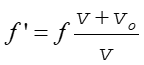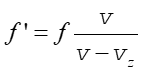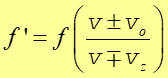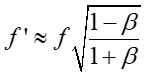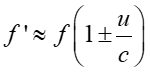13.8 Zjawisko Dopplera
|
Prawo, zasada, twierdzenie Zjawisko Dopplera polega na pozornej zmianie częstotliwości fali z powodu ruchu obserwatora lub źródła fali. |
W pracy z 1842 r, Christian Doppler
zwrócił uwagę, że barwa świecącego ciała (częstotliwość wysyłanego
promieniowania) musi się zmieniać z powodu ruchu względnego
obserwatora lub źródła. Zjawisko Dopplera występuje dla wszystkich fal;
my szczegółowo rozważymy je dla fal dźwiękowych. Ograniczymy się do
przypadku ruchu źródła i obserwatora wzdłuż łączącej ich
prostej.
Rozpatrzmy sytuację gdy źródło dźwięku spoczywa, a
obserwator porusza się w kierunku źródła z prędkością vo
(względem ośrodka). Jeżeli fale o długości λ
rozchodzą się z prędkością v to w czasie t dociera
do nieruchomego obserwator 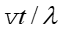 fal. Jeżeli obserwator porusza się w kierunku źródła (wychodzi
falom na przeciw) to odbiera jeszcze dodatkowo
fal. Jeżeli obserwator porusza się w kierunku źródła (wychodzi
falom na przeciw) to odbiera jeszcze dodatkowo 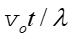 fal. W związku z tym częstotliwość f ' odbierana (słyszana) przez obserwatora
fal. W związku z tym częstotliwość f ' odbierana (słyszana) przez obserwatora
|
(13.37) |
|
(13.38) |
Obserwator rejestruje wyższą częstotliwość niż częstotliwość źródła. Kiedy obserwator oddala się od źródła należy w powyższych wzorach zmienić znak prędkości obserwatora vo. W tym przypadku częstotliwość zmniejsza się.
Analogicznie możemy przestudiować przypadek źródła poruszającego się z prędkością vz względem nieruchomego obserwatora (i względem ośrodka). Otrzymujemy wtedy zależność
|
(13.39) |
dla przypadku źródła zbliżającego się do obserwatora. Gdy źródło oddala się to w powyższym wzorze zmieniamy znak prędkości źródła vz. Zwróćmy uwagę, że zmiany częstotliwości zależą od tego czy porusza się źródło czy obserwator. Wzory (13.38) i (13.39) dają inny wynik dla jednakowych prędkości obserwatora i źródła.
W sytuacji kiedy porusza się zarówno źródło jak i obserwator otrzymujemy zależność będącą połączeniem wzorów (13.39) i (13.40)
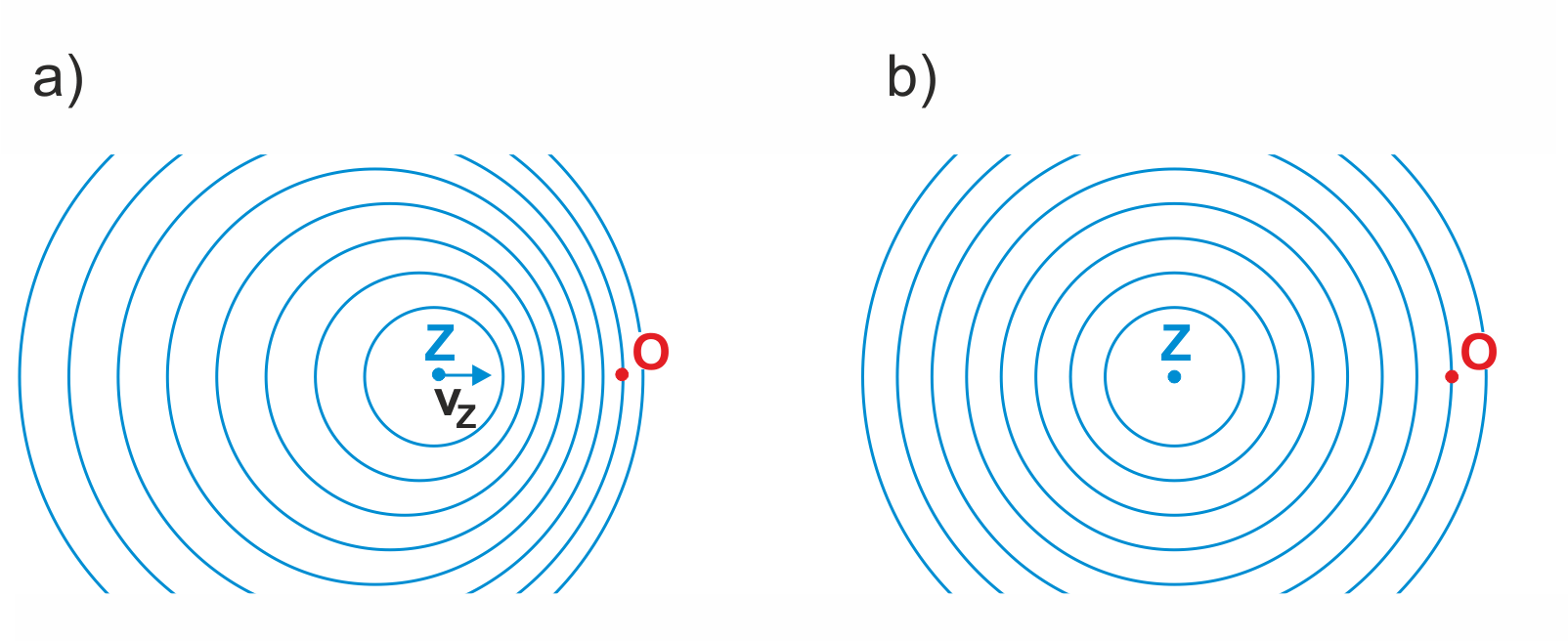
Rys. 13.16. Fale wysyłane przez źródło Z: (a) poruszające się z prędkością vz w stronę obserwatora O; (b) przez nieruchome źródło
|
(13.40) |
Znaki "górne" w liczniku i mianowniku odpowiadają zbliżaniu się źródła i obserwatora, a znaki "dolne" ich oddalaniu się. Powyższe wzory są słuszne gdy prędkości źródła i obserwatora są mniejsze od prędkości dźwięku.
|
Symulacje komputerowe Korzystając z załączonego programu możesz prześledzić zjawisko Dopplera dla źródła i obserwatora poruszających się wzdłuż łączącej ich prostej. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera. |
|
Ćwiczenie Typowym przykładem efektu Dopplera jest zmiana częstotliwości dźwięku klaksonu samochodu przejeżdżającego koło nas. Słyszymy, że klakson ma wyższy ton gdy samochód zbliża się do nas, a niższy gdy się oddala. Załóżmy, że podczas mijania nas przez samochód rejestrujemy obniżenie częstotliwości klaksonu o 15%. Na podstawie tej informacji sprawdź czy samochód nie przekroczył dozwolonej, poza obszarem zabudowanym, prędkości 90 km/h. Prędkość dźwięku przyjmij równą 340 m/s. Sprawdź obliczenia i wynik. |
Zjawisko Dopplera obserwujemy również w przypadku fal elektromagnetycznych, a więc i świetlnych. Opis tego zjawiska dla światła jest inny niż dla fal dźwiękowych. Dla fal dźwiękowych otrzymaliśmy dwa wyrażenia (13.38) i (13.39) na zmianę częstotliwości fali w zależności od tego czy to źródło czy też obserwator poruszają się względem ośrodka przenoszącego drgania (powietrza). Do rozchodzenia się światła nie jest potrzebny ośrodek (światło może rozchodzić się w próżni) ponadto, zgodnie ze szczególną teorią względności Einsteina, prędkość światła nie zależy od układu odniesienia i dlatego częstotliwość fali świetlnej odbieranej przez obserwatora zależy tylko od prędkości względnej źródła światła i obserwatora. Jeżeli źródło i obserwator poruszają się wzdłuż łączącej ich prostej to
|
(13.41) |
gdzie ![]() .
W tej zależności u jest prędkością względną źródła względem
odbiornika, a c prędkością światła. Dla małych wartości prędkości
względnej
.
W tej zależności u jest prędkością względną źródła względem
odbiornika, a c prędkością światła. Dla małych wartości prędkości
względnej ![]() powyższy
wzór przyjmuje postać
powyższy
wzór przyjmuje postać
|
(13.42) |
Znak "+" odnosi się do wzajemnego zbliżania
się źródła i obserwatora, a znak "−"
do ich wzajemnego oddalania się. Zbliżaniu towarzyszy więc wzrost częstotliwości
(dla światła oznacza to przesunięcie w stronę fioletu), a oddalaniu się
obniżenie częstotliwości (dla światła oznacza to przesunięcie w stronę
czerwieni).
Zjawisko to ma liczne zastosowania: na przykład w astronomii służy do
określenia prędkości odległych świecących ciał niebieskich. Porównujemy
długości fal światła wysyłanego przez pierwiastki tych obiektów z długościami
fal światła wysyłanego przez takie same pierwiastki znajdujące się na
Ziemi. To właśnie szczegółowe badania przesunięć ku czerwieni w
widmach odległych galaktyk wykazały, że Wszechświat rozszerza się.


 Dudnienia, modulacja amplitudy
Dudnienia, modulacja amplitudy