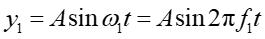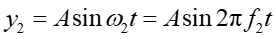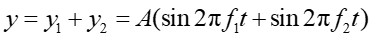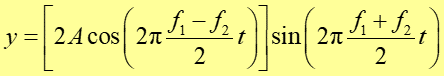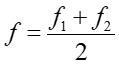13. Fale w ośrodkach sprężystych
• Spis treści  
• Zjawisko Dopplera  
•   Analiza fal złożonych

13.7 Dudnienia, modulacja amplitudy

  Gdy omawialiśmy fale stojące to mieliśmy do czynienia z sytuacją, w której dodawanie (superpozycja) zaburzeń dało w wyniku falę o amplitudzie stałej w czasie ale zależnej od położenia cząstki drgającej x. Jest to ilustracja tzw. interferencji w przestrzeni. Teraz rozpatrzmy przypadek interferencji w czasie. W tym celu rozpatrzymy, w danym punkcie przestrzeni x, wynik nakładania się dwóch biegnących w tym samym kierunku fal o jednakowych amplitudach ale nieznacznie różnych częstotliwościach. Drgania harmoniczne danej cząstki ośrodka (w zadanym punkcie x) wywołane przez te fale mają postać

Ze wzoru na sumę sinusów otrzymujemy

Równanie to ma postać . Drgania wypadkowe można więc uważać za drgania o częstotliwości

(która jest średnią częstotliwości dwóch fal) i o amplitudzie A' (wyrażenie w nawiasie kwadratowym w równaniu 13.34). Zauważ, że amplituda zmienia się w czasie z częstotliwością

Jeżeli częstotliwości f₁ i f₂ są bliskie siebie to amplituda zmienia się powoli (f_amp. jest mała). Mówimy, że mamy do czynienia z modulacją amplitudy (AM - amplitude modulation). Naturalną modulację amplitudy dla fal dźwiękowych możemy usłyszeć gdy dwie struny instrumentu są nastrojone na niewiele różniące się tony. Gdy obie te struny wydają równocześnie dźwięk (na przykład uderzono dwa sąsiednie klawisze fortepianu) to usłyszymy tak zwane dudnienia przejawiające się jako zmiana głośności (rysunek 13.15).
Zastosowanie modulacji ma na celu wprowadzenie do procesu potrzebnej informacji, która ma być przesłana za pomocą fal. Modulacja amplitudy jest najstarszym i najbardziej rozpowszechnionym (obok modulacji częstotliwości FM) sposobem przesyłania informacji za pomocą fal radiowych.

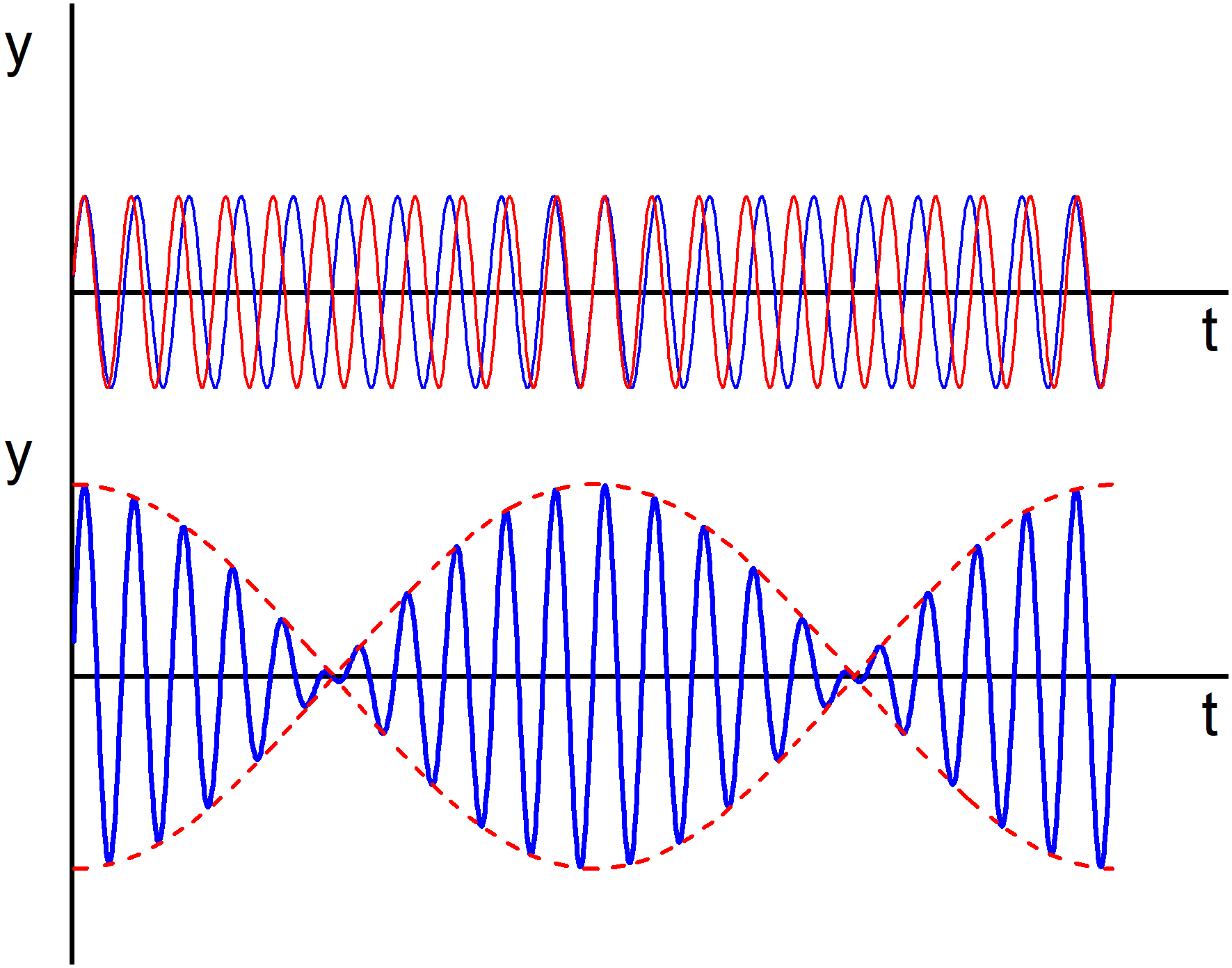
 Rys. 13.15. Nałożenie się drgań harmonicznych pokazanych na górnym wykresie daje w wyniku
drganie o zmiennej w czasie amplitudzie (obwiednia dolnego wykresu)