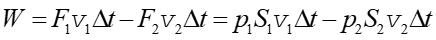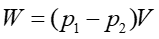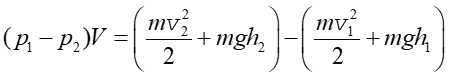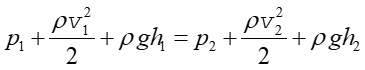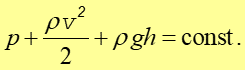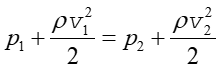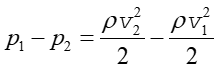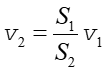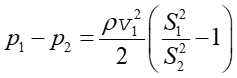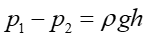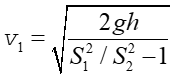Równanie Bernoulliego

14.5 Równanie Bernoulliego

Rozważmy, pokazany na rysunku 14.9, nielepki, ustalony, nieściśliwy przepływ płynu w strudze. Płyn na rysunku przemieszcza się w stronę prawą. W czasie Δt powierzchnia S₁ przemieszcza się o odcinek v₁Δt. Analogicznie powierzchnia S₂ przemieszcza się o odcinek v₂Δt. Na powierzchnię S₁ działa siła F₁ = p₁S₁, a na powierzchnię S₂ siła F₂ = p₂S₂.

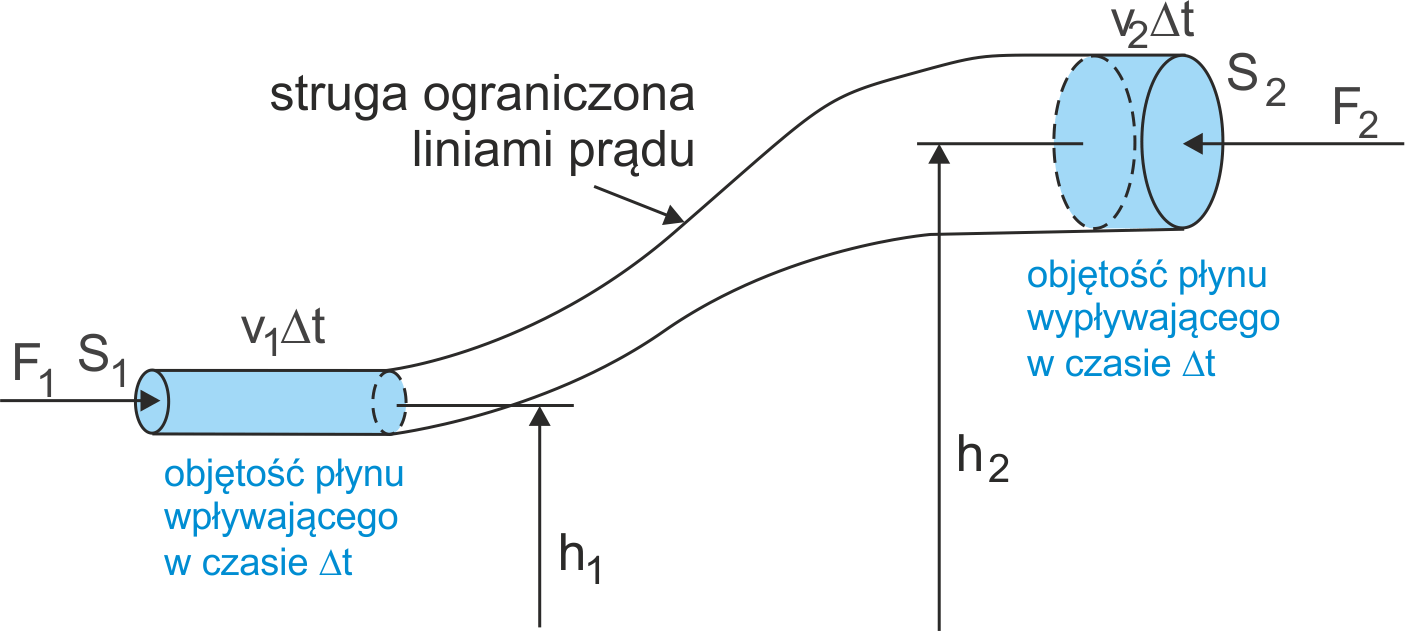
Rys. 14.9. Wyprowadzenie równania Bernoulliego

Skorzystamy teraz z twierdzenia o pracy i energii, które mówi, że praca wykonana przez wypadkową siłę jest równa zmianie energii układu. Siłami, które wykonują pracę są F₁ i F₂. Obliczamy więc całkowitą pracę

(14.19)

Ponieważ w czasie Δt ta sama objętość płynu V wpływa do strugi i z niej wypływa więc

(14.20)

Obliczoną pracę porównujemy ze zmianą energii strugi

(14.21)

gdzie m jest masą przemieszczonej objętości V płynu. Dzieląc stronami równanie (14.21) przez objętość V, a następnie wprowadzając gęstość cieczy ρ = m/V można, grupując odpowiednio wyrazy, przekształcić to równanie do postaci

(14.22)

Ponieważ nasze rozważania odnosiły się do dowolnych dwóch położeń, możemy opuścić wskaźniki i napisać

(14.23)

Równanie to nosi nazwę równania Bernoulliego dla przepływu ustalonego, nielepkiego i nieściśliwego. Jest to podstawowe równanie mechaniki płynów. Wyraża fakt, że z przepływem płynu związane jest (oprócz ciśnienia statycznego) ciśnienie dynamiczne .

Wynika z niego, że przepływ cieczy w strudze może być wywołany różnicą ciśnień na końcach strugi lub różnicą poziomów tych końców.

Zilustrujmy to prostym przykładem pompki wodnej stosowanej na przykład w akwarystyce. W tym urządzeniu woda z akwarium jest przepompowywana przez układ filtrów i odprowadzana z powrotem do akwarium. Po drodze woda jest przepuszczana przez przewężenie w rurce tak jak na rysunku 14.10.

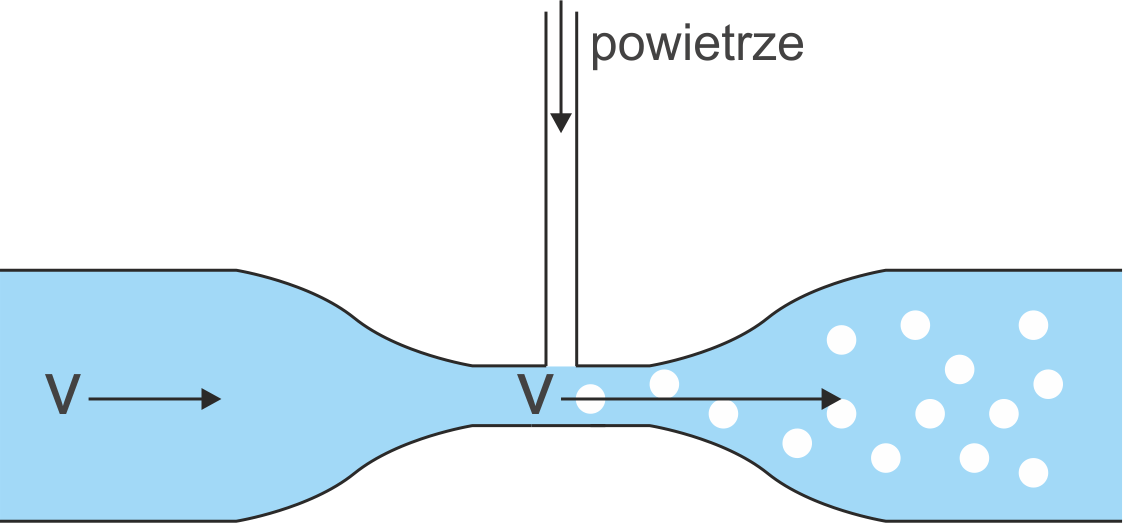
Rys. 14.10. Pompka wodna

Prędkość wody w przewężeniu jest (zgodnie z równaniem ciągłości) większa niż w rurce. Natomiast zgodnie z równaniem Bernoulliego, w poziomej rurce (h = const.) , więc gdy rośnie prędkość v i płyn jest nieściśliwy (stała gęstość), to p maleje i w przewężeniu ciśnienie jest mniejsze niż w pozostałej części rurki. Jeżeli to przewężenie jest dostatecznie małe to ciśnienie może być niższe od atmosferycznego, a to oznacza, że przez otwór w przewężeniu woda nie będzie uciekać tylko z zewnątrz będzie zasysane powietrze. W ten sposób woda będzie nie tylko filtrowana ale jeszcze dodatkowo napowietrzana.

Ćwiczenie
Spróbuj samodzielnie wykonać bardzo proste doświadczenie. Weź dwie kartki papieru i trzymaj je ustawione równolegle do siebie w niewielkiej odległości (np. 1-2 cm). Następnie dmuchnij między kartki. Okazuje się, że kartki nie rozchylają się, a zbliżają do siebie, sklejają się. Spróbuj wyjaśnić przyczynę tego zjawiska.

Równanie Bernoulliego może być wykorzystane do wyznaczenia prędkości płynu na podstawie pomiaru ciśnienia. Ponownie posługujemy się rurką z przewężeniem, do której przymocowano tak jak na rysunku 14.11, dwie pionowe rurki A i B służące do pomiaru ciśnienia.

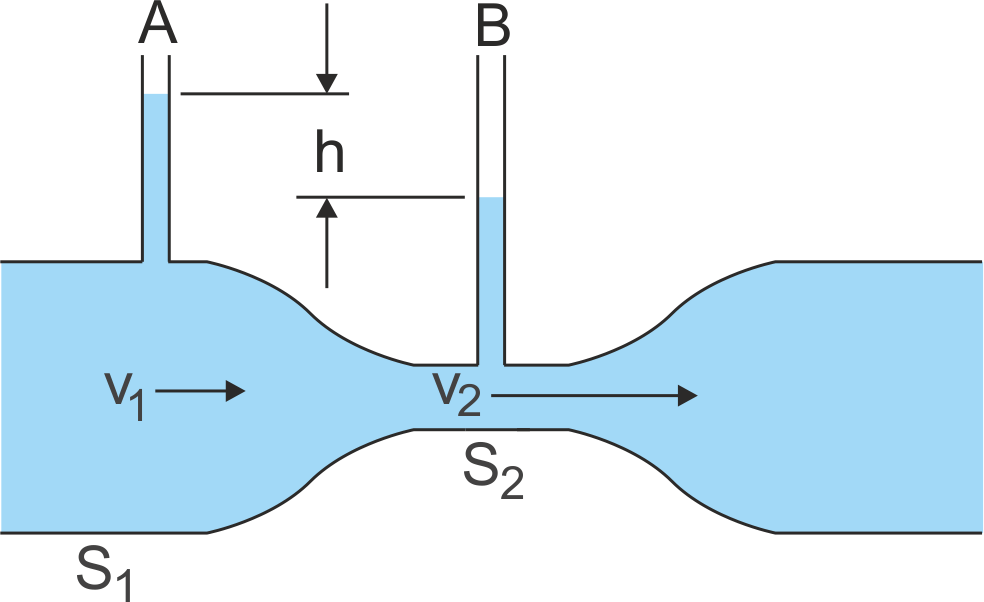
Rys. 14.11. Pomiar prędkości płynu metodą Venturiego

Stosując równanie Bernoulliego dla punktów, w których prędkość płynu wynosi odpowiednio v₁ i v₂ (przewężenie) otrzymujemy

(14.24)

Ponieważ v₁ < v₂ więc ciśnienie w przewężeniu jest mniejsze niż w rurce p₂ < p₁. Różnica ciśnień zgodnie z równaniem (14.24) wynosi

(14.25)

Z równania ciągłości wynika, że

(14.26)

Podstawiając tę zależność do równania (14.25) otrzymujemy

(14.27)

Równocześnie tę samą różnicę ciśnień można wyznaczyć z różnicy poziomów płynu w rurkach A i B (rysunek 14.11)

(14.28)

Porównując powyższe dwa wzory możemy wyznaczyć prędkość v₁ w rurce

(14.29)

Metoda pomiaru prędkości płynu oparta na wyznaczeniu różnicy wysokości płynu w dwóch pionowych rurkach nosi nazwę metody Venturiego.

Ćwiczenie
W zbiorniku wody na głębokości h znajduje się otwór przez który wycieka woda. Posługując się równaniem Bernoulliego oblicz prędkość v z jaką wycieka woda. Sprawdź obliczenia i wynik.