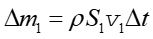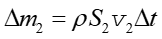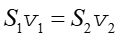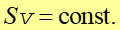14. Statyka i dynamika płynów
• Spis treści  
• Równanie Bernoulliego  
•   Prawo Pascala i prawo Archimedesa

14.4 Ogólny opis przepływu płynów

   Przejdziemy teraz do opisu ruchu płynu czyli zajmiemy się dynamiką płynów. Znane są dwa podejścia do opisu ruchu płynu. Możemy albo zająć się opisem ruchu poszczególnych cząsteczek płynu albo opisywać gęstość płynu i jego prędkość w każdym punkcie przestrzeni w funkcji czasu. Oznacza to, że koncentrujemy się na wybranym punkcie przestrzeni, w którym definiujemy funkcje ρ(x,y,z,t) oraz v(x,y,z,t).

Na wstępie poznamy ogólne pojęcia charakteryzujące przepływ:

• Przepływ może być ustalony (laminarny) lub nieustalony . Ruch płynu jest ustalony, gdy prędkość płynu v w dowolnie wybranym punkcie jest stała w czasie tzn. każda cząsteczka przechodząca przez dany punkt zachowuje się tak samo. Warunki takie osiąga się przy niskich prędkościach przepływu.


• Przepływ może być wirowy lub bezwirowy . Przepływ jest bezwirowy, gdy w żadnym punkcie cząsteczka nie ma wypadkowej prędkości kątowej.


• Przepływ może być ściśliwy lub nieściśliwy . Przepływ jest nieściśliwy gdy gęstość płynu jest stała. Zazwyczaj przepływ cieczy jest nieściśliwy. Również przepływ gazu może być w pewnych warunkach nieściśliwy. Przykładem może tu być ruch powietrza względem skrzydeł samolotu podczas lotu z prędkością mniejszą od prędkości dźwięku.


• Przepływ może być lepki lub nielepki . Lepkość w ruchu płynów jest odpowiednikiem tarcia w ruchu ciał stałych. Charakteryzuje opór płynów przeciw płynięciu pod działaniem sił zewnętrznych. Lepkość jest istotną cechą wielu produktów na przykład smarów.

W naszych rozważaniach ograniczymy się do przepływów ustalonych, bezwirowych, nieściśliwych i nielepkich.

W przepływie ustalonym v jest stała w czasie w danym punkcie. Oznacza to, że każda cząstka przechodząca przez dowolny punkt ma taką samą prędkość np. v₁. Tak samo jest w kolejnym punkcie gdzie każda cząstka ma prędkość v₂. Dotyczy to wszystkich punktów. Oznacza to, że wystarczy prześledzić tor jednej cząstki, a będziemy znali tor każdej cząstki przechodzącej przez dany punkt. Tor tej cząstki nazywamy linią prądu (rysunek 14.7). Linia prądu jest równoległa do prędkości płynu. Żadne linie prądu nie mogą się przecinać bo istniałaby niejednoznaczność w wyborze drogi przez cząstkę (przepływ nie byłby ustalony).

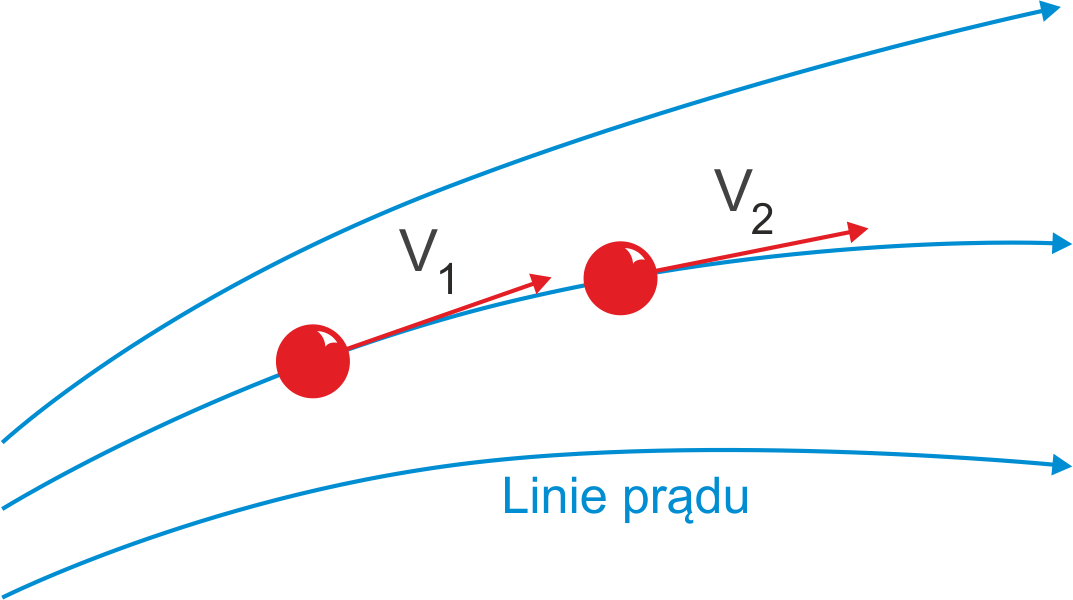
 Rys. 14.7. Linie prądu

Jeżeli wybierzemy pewną skończoną liczbę linii prądu to taką wiązkę nazywamy strugą prądu . Brzegi składają się z linii prądu, a ponieważ linie prądu są równoległe do prędkości więc płyn nie przepływa przez brzegi strugi. Płyn wchodzący jednym końcem strugi musi opuścić ją drugim tak jak w rurce. Na rysunku 14.8 prędkość cząstek w punkcie P₁ wynosi v₁, a pole przekroju strugi S₁. W punkcie P₂ mamy odpowiednio prędkość v₂ i pole przekroju S₂.

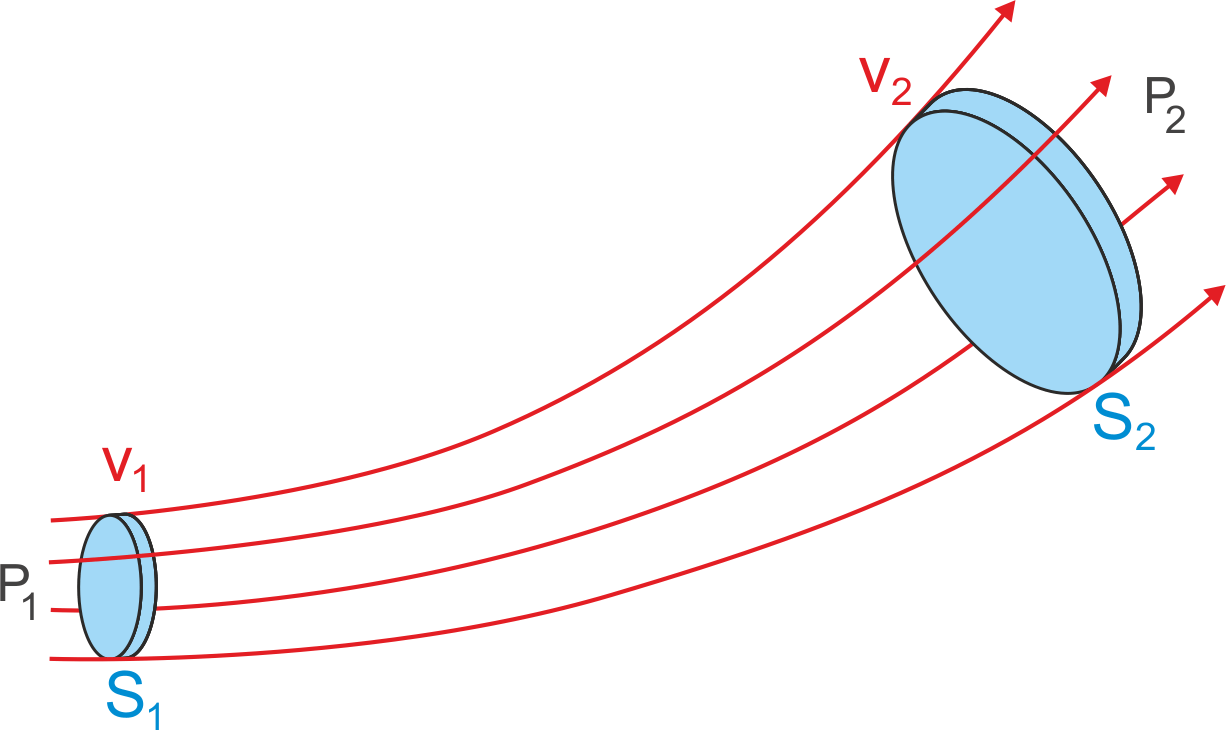
 Rys. 14.8. Struga prądu

W czasie Δt cząstka płynu przebywa odległość równą vΔt. Masa płynu przechodzącego przez S₁ w czasie Δt wynosi

gdzie S₁v₁Δt stanowi objętość elementu płynu. Analogicznie masa płynu przepływającego przez powierzchnię S₂ w czasie Δt jest równa

Ponieważ płyn jest nieściśliwy więc jego gęstość jest taka sama w punkcie P₁ i P₂. Ponadto między tymi punktami płyn nie może opuścić strugi więc strumienie mas przepływające przez obie powierzchnie muszą być sobie równe. Zatem

Otrzymany związek nosi nazwę równania ciągłości. Wynika z niego, że

Linie prądu muszą się zagęszczać w węższej części, a rozrzedzać w szerszej. To znaczy, rzadko rozmieszczone linie oznaczają obszary niskiej prędkości, linie rozmieszczone gęsto obszary wysokiej prędkości.