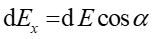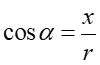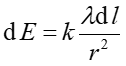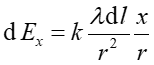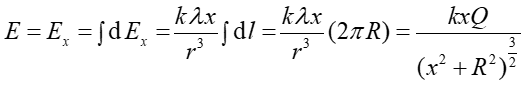Pole elektryczne na osi pierścienia

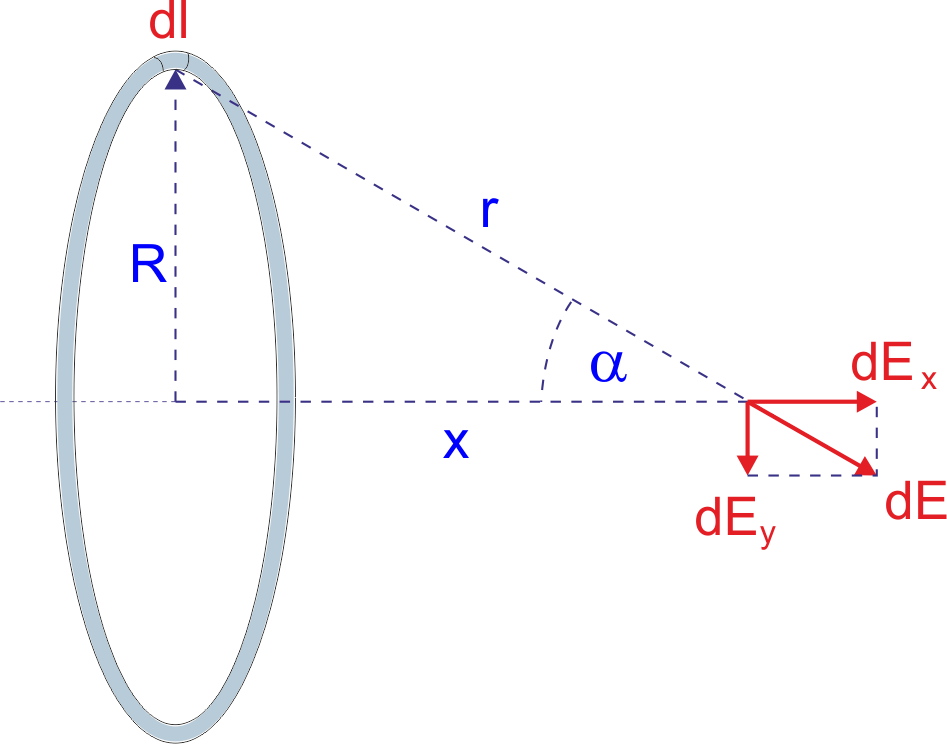
Z zasady superpozycji możemy również skorzystać dla ciągłych rozkładów ładunków. Jako przykład rozpatrzymy jednorodnie naładowany pierścień o promieniu R i całkowitym ładunku Q pokazany na rysunku poniżej. Chcemy obliczyć pole elektryczne na osi pierścienia w odległości x od jego środka.

Rys. 1. Pierścień naładowany jednorodnie ładunkiem Q

(1)

oraz

(2)

Jeżeli λ = Q / 2πR jest liniową gęstością ładunku (ilością ładunku na jednostkę długości) to element dl zawiera ładunek dQ = λdl i natężenie pola od tego elementu jest równe

(3)

oraz

(4)

Pole elektryczne całego pierścienia otrzymujemy zgodnie z zasadą superpozycji sumując (całkując) pola od wszystkich elementów pierścienia. Zwróćmy uwagę, że składowe pionowe dE_y elementów leżących po przeciwnych stronach pierścienia znoszą się wzajemnie więc

(5)

Zauważmy, że w środku pierścienia (x = 0) E = 0, a w bardzo dużej odległości od pierścienia (x >> R ) pole zmierza do wartości E → kQ/x² takiej jak pole ładunku punktowego w tej odległości.

Jedną z zalet posługiwania się pojęciem pola elektrycznego jest to, że nie musimy zajmować się szczegółami źródła pola. Powyższy przykład pokazuje, że z pomiaru pola elektrycznego nie możemy ustalić jaki jest rozkład ładunków będący źródłem tego pola (ładunek punktowy czy odległy naładowany pierścień).