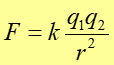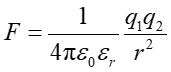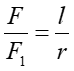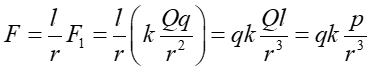Ładunek elektryczny17.2 Prawo Coulomba
Siłę wzajemnego oddziaływania
dwóch naładowanych punktów materialnych (ładunków
punktowych 
)
znajdujących się w odległości r od siebie w próżni opisuje
prawo Coulomba
|
Prawo, zasada, twierdzenie Każde dwa ładunki punktowe q1 i q2 oddziaływają wzajemnie siłą wprost proporcjonalną do iloczynu tych ładunków, a odwrotnie proporcjonalną do kwadratu odległości między nimi. |
|
(17.1) |
gdzie stała 
.
Współczynnik ε0 = 8.854·10−12 C2/(Nm2)
nosi nazwę przenikalności elektrycznej próżni. Oddziaływanie
ładunków zależy od ośrodka w jakim znajdują się ładunki. Fakt ten
uwzględniamy wprowadzając stałą materiałową εr, zwaną względną
przenikalnością elektryczną ośrodka tak, że prawo Coulomba przyjmuje postać
|
(17.2) |
Wartości εr dla wybranych substancji zestawiono w tabeli 17.1.
Tab. 17.1. Względne przenikalności elektryczne wybranych substancji
| Ośrodek | εr |
|---|---|
| próżnia | 1 |
| powietrze | 1.0006 |
| parafina | 2 |
| teflon | 2.1 |
| polietylen | 2.3 |
| papier | 3.5 |
| szkło (pyrex) | 4.5 |
| porcelana | 6.5 |
| woda | 81 |
| TiO2 | 100 |
|
Ćwiczenie Spróbuj teraz korzystając z prawa Coulomba obliczyć siłę przyciągania elektrostatycznego pomiędzy elektronem i protonem w atomie wodoru. Przyjmij r = 5·10−11 m. Porównaj tę siłę z siła przyciągania grawitacyjnego między tymi cząstkami. Masa protonu mp = 1.67·10−27 kg, a masa elektronu me = 9.11·10−31 kg. Stała grawitacyjna G = 6.7·10−11 Nm2/kg2. Sprawdź obliczenia i wynik. |
|
Ćwiczenie Jeżeli rozwiązałeś powyższy przykład to postaraj się rozwiązać następujący problem. Cała materia składa się z elektronów, protonów i obojętnych elektrycznie neutronów. Jeżeli oddziaływania elektrostatyczne pomiędzy naładowanymi cząstkami (elektronami, protonami) są tyle razy większe od oddziaływań grawitacyjnych to dlaczego obserwujemy słabą siłę grawitacyjną działająca pomiędzy dużymi ciałami, np. Ziemią i spadającym kamieniem, a nie siłę elektrostatyczną? |
Zasada superpozycji
|
Prawo, zasada, twierdzenie Gdy mamy do czynienia z kilkoma naładowanymi ciałami, siłę wypadkową, analogicznie jak w przypadku siły grawitacyjnej, obliczamy dodając wektorowo poszczególne siły dwuciałowe. |
Przykład
Dipol elektryczny składa się z dwóch ładunków +Q i -Q oddalonych od siebie o l. Obliczmy siłę jaka jest wywierana na dodatni ładunek q umieszczony na symetralnej dipola, tak jak pokazano na rysunku 17.1.
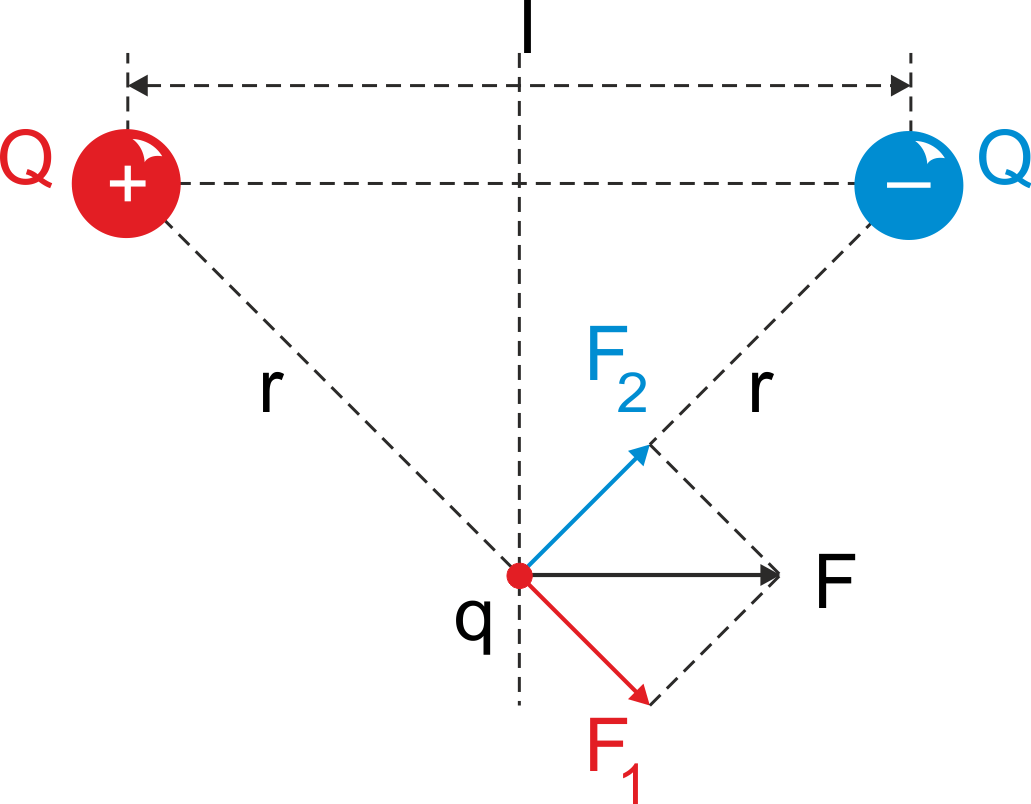
Rys. 17.1. Siły wywierane przez dipol elektryczny na ładunek q
Z podobieństwa trójkątów wynika, że
|
(17.3) |
Korzystając z prawa Coulomba otrzymujemy
|
(17.4) |
gdzie p = Ql
jest momentem dipolowym .