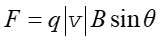22.1 Siła magnetyczna
W pobliżu przewodników z prądem elektrycznym i magnesów działają siły magnetyczne. Spotykamy je gdy mamy do czynienia z magnesem trwałym, elektromagnesem, silnikiem elektrycznym, prądnicą, czy monitorem komputerowym. Magnesem jest sama Ziemia. Jej działanie na igłę kompasu jest znane od Starożytności. Natomiast w XIX w. Oersted stwierdził, że kompas ulega również wychyleniu w pobliżu przewodnika, w którym płynie prąd i zmienia kierunek wychylenia wraz ze zmianą kierunku prądu (rysunek poniżej).
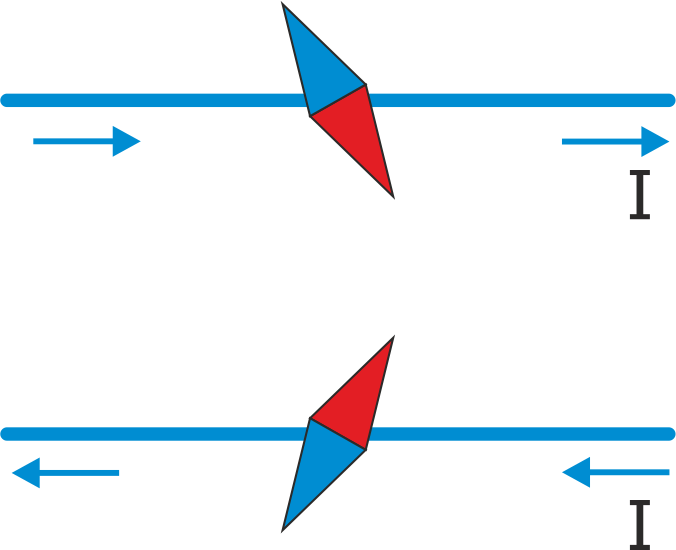
Rys. 22.1. Doświadczenie Oersteda
To oddziaływanie pomiędzy prądem i magnesem opisujemy wprowadzając pojęcie
pola magnetycznego ![]() .
Przypomnijmy, że w przypadku sił grawitacyjnych posługiwaliśmy się
pojęciem natężenia pola grawitacyjnego γ,
gdzie
.
Przypomnijmy, że w przypadku sił grawitacyjnych posługiwaliśmy się
pojęciem natężenia pola grawitacyjnego γ,
gdzie ![]() ,
a w przypadku sił elektrycznych pojęciem natężeniu pola elektrycznego E, gdzie
,
a w przypadku sił elektrycznych pojęciem natężeniu pola elektrycznego E, gdzie
![]() .
Natomiast siłę działającą na ładunek q poruszający się w polu magnetycznym z prędkością
v wiążemy z indukcją magnetyczną B
.
Natomiast siłę działającą na ładunek q poruszający się w polu magnetycznym z prędkością
v wiążemy z indukcją magnetyczną B ![]() .
Związek pomiędzy siłą magnetyczną a indukcją magnetyczną B zapisujemy w postaci równania wektorowego
.
Związek pomiędzy siłą magnetyczną a indukcją magnetyczną B zapisujemy w postaci równania wektorowego
|
Definicja |
|
(22.1) |
Siłę tę nazywamy siłą Lorentza ![]() ,
a powyższe równanie definiuje indukcję pola magnetycznego B.
,
a powyższe równanie definiuje indukcję pola magnetycznego B.
|
Jednostki W układzie SI jednostką indukcji B jest tesla; (T); 1T = 1N/(Am) = 1Vs/m2. |
Poniższa tabela pozwala na zorientowanie się w zakresie pól magnetycznych dostępnych w przyrodzie i wytwarzanych przez różne urządzenia.
Typowe wartości oporu wewnętrznego różnych źródeł są zestawione w tabeli 21.2 poniżej.
Tab. 21.2. Zakres pól magnetycznych
| Źródło pola B | Bmaks. [T] |
|---|---|
| Pracujący mózg | 10−13 |
| Ziemia | ≈ 4·10−5 |
| Elektromagnes | 2 |
| Cewka nadprzewodząca | 20 |
| Cewka impulsowa | 70 |
| Gwiazda neutronowa | ≈ 108 |
Zgodnie z definicją iloczynu wektorowego, z równania (22.1) wynika, że wartość siły działająca na naładowaną cząstkę w polu magnetycznym jest równa
|
(22.2) |
gdzie θ jest kątem pomiędzy wektorami v i B.
Siła jest równa zeru gdy cząstka nie porusza się oraz gdy wektor prędkości v jest równoległy do wektora B (θ = 0º) lub do niego antyrównoległy (θ = 180º). Natomiast maksimum siły występuje gdy wektor prędkości v jest prostopadły do wektora B (θ = 90º).
Równanie (22.1) określa również kierunek i zwrot wektora siły F. Z definicji iloczynu wektorowego wynika, że wektor F jest prostopadły do płaszczyzny wyznaczonej przez wektory v i B. Zwrot jego jest określony regułą śruby prawoskrętnej lub regułą prawej ręki. Jeżeli palce prawej ręki zginają się w kierunku obrotu wektora v do wektora B (po mniejszym łuku) to kciuk wskazuje kierunek wektora F ~ v x B tak jak na rysunku poniżej
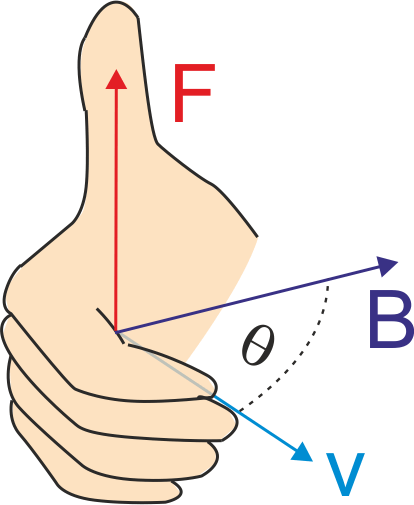
Rys. 22.2. Reguła prawej ręki wyznacza kierunek działania siły w polu magnetycznym
Zwrot wektora F pokazany na rysunku powyżej odpowiada dodatniemu ładunkowi q. Dla ładunku ujemnego kierunek jest ten sam ale zwrot przeciwny.
|
Ćwiczenie Spróbuj teraz określić siłę działająca na dodatni ładunek poruszający się w polu magnetycznym tak jak pokazano na rysunku poniżej. W każdej z czterech pokazanych konfiguracji zaznaczono wektor prędkości ładunku i wektor indukcji magnetycznej. Spróbuj narysować wektor siły. Skorzystaj z definicji iloczynu wektorowego. Sprawdź obliczenia i wynik. |


 Obwody prądu stałego
Obwody prądu stałego