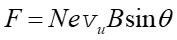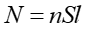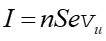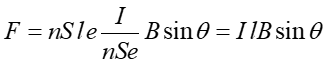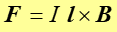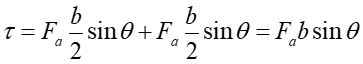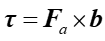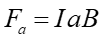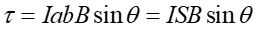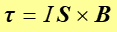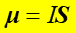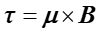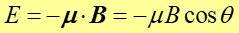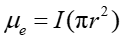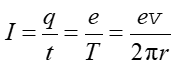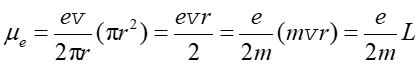22. Pole magnetyczne
• Spis treści  
• Efekt Halla  
•   Ruch naładowanych cząstek w polu magnetycznym

22.4 Działanie pola magnetycznego na przewodnik z prądem

  Ponieważ siła magnetyczna działa na ładunki w ruchu zatem działa na cały przewodnik z prądem

gdzie N jest liczbą elektronów zawartych w danym przewodniku o długości l i przekroju poprzecznym S, a v_u ich średnią prędkością unoszenia.
Jeżeli n jest koncentracją elektronów (ilością elektronów w jednostce objętości) to

Zgodnie z wzorem (21.5) natężenie prądu w przewodniku wynosi

Podstawiając te wyrażenia do wzoru na siłę otrzymujemy

lub w zapisie wektorowym

Na rysunku poniżej zaznaczona jest siła działająca w polu magnetycznym na przewodnik, w którym płynie prąd o natężeniu I. W polu magnetycznym znajduje się odcinek l przewodnika, a wektor długości l ma zwrot zgodny ze zwrotem prądu.

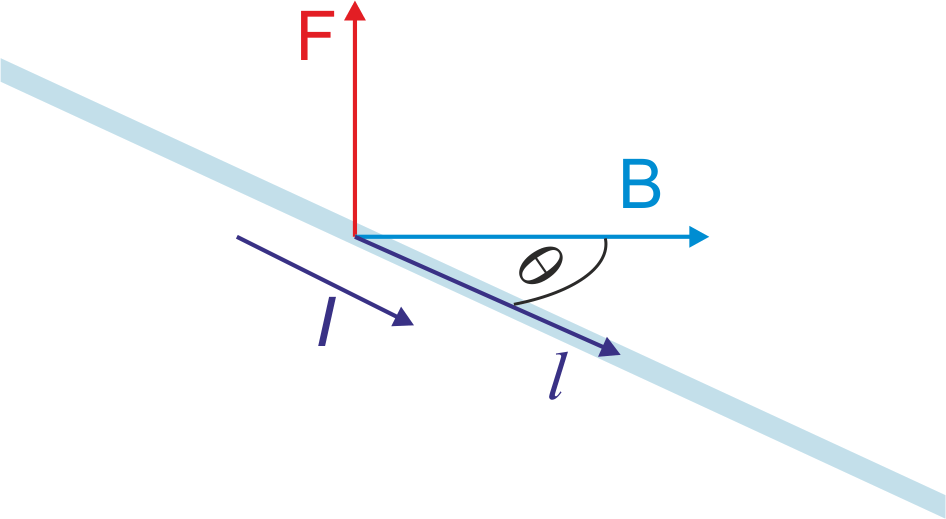
 Rys. 22.8. Siła działająca w polu magnetycznym na przewodnik z prądem

Równanie jest równoważne równaniu w tym sensie, że każde z nich definiuje indukcję pola magnetycznego B. Jednak w praktyce łatwiej jest zmierzyć siłę działającą na przewodnik niż na pojedynczy ładunek.

Obwód z prądem

Rozważymy teraz działanie pola magnetycznego na zamknięty obwód z prądem. W tym celu rozpatrzmy prostokątną ramkę o bokach a i b umieszczoną w jednorodnym polu magnetycznym o indukcji B. Taka ramka stanowi podstawowy element silnika elektrycznego.
Przez ramkę płynie prąd o natężeniu I, a normalna do płaszczyzny ramki tworzy kąt θ z polem B tak jak na rysunku 22.9.

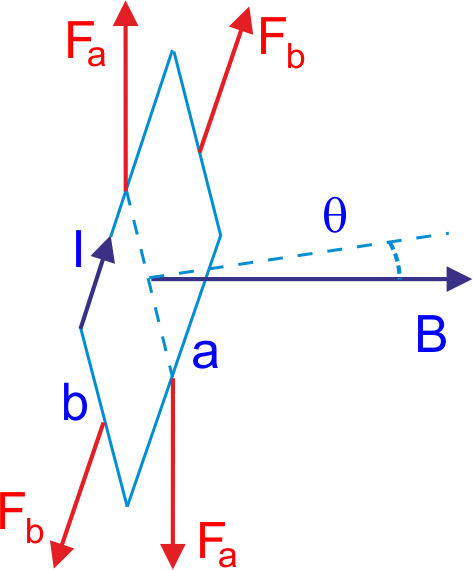
 Rys. 22.9. Działanie pola magnetycznego B na ramkę z prądem I

Rozpatrujemy siłę działającą na każdy z boków. Zauważmy, że siły F_b działające na boki b znoszą się wzajemnie. Siły F_a działające na boki a też się znoszą ale tworzą parę sił dającą wypadkowy moment siły obracający ramkę

lub w zapisie wektorowym (na podstawie definicji iloczynu wektorowego)

Siła F_a wynosi

gdzie S = ab jest powierzchnią ramki. Równanie (22.17) możemy zapisać w postaci wektorowej

gdzie S jest wektorem powierzchni.

Magnetyczny moment dipolowy

Wielkość wektorową

nazywamy magnetycznym momentem dipolowym . Wektor μ jest prostopadły do płaszczyzny ramki z prądem.

Pole magnetyczne działa więc na ramkę z prądem momentem skręcającym

obracając ją tak jak igłę kompasu, która umieszczona w polu magnetycznym obraca się ustawiając zgodnie z polem.
Położenie równowagi ramki występuje dla θ  = 0 tj. gdy moment dipolowy μ jest równoległy do pola magnetycznego B (ramka jest ustawiona prostopadle do pola). Ramka zachowuje się więc tak jak igła kompasu czyli dipol magnetyczny.

Obracając dipol magnetyczny pole magnetyczne wykonuje pracę i wobec tego dipol posiada energię potencjalną. Można pokazać, że energia potencjalna dipola magnetycznego związana z jego orientacją w zewnętrznym polu magnetycznym dana jest równaniem

Widzimy, że energia osiąga minimum dla momentu dipolowego μ równoległego do zewnętrznego pola magnetycznego B, a maksimum gdy moment dipolowy jest skierowany przeciwnie do pola (rysunek 22.10).

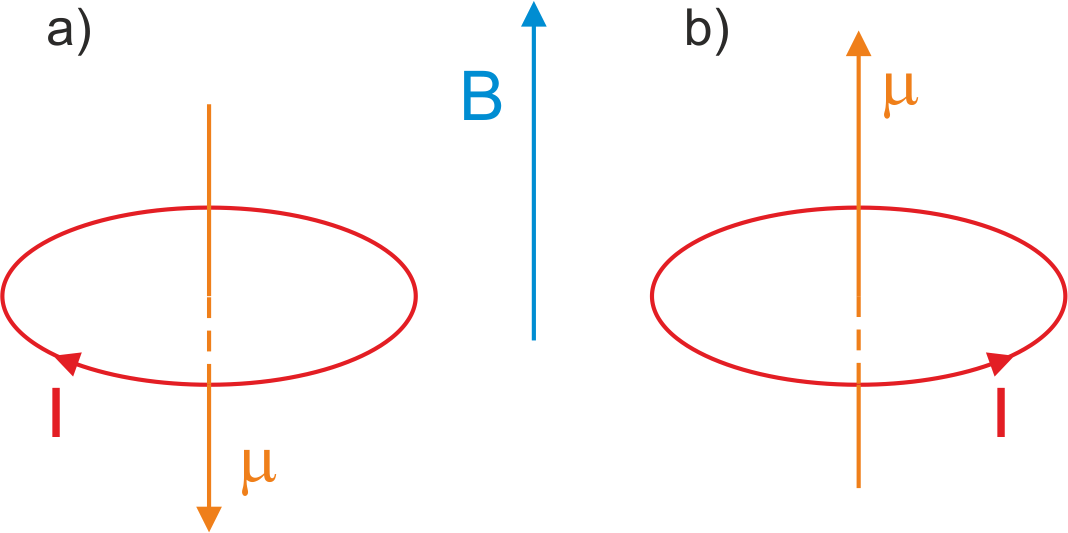
 Rys. 22.10. Ustawienie momentu dipolowego (pętli z prądem) w zewnętrznym polu magnetycznym odpowiadające a) maksimum, b) minimum energii

Jak już mówiliśmy ramka z prądem jest przykładem dipola magnetycznego. Taką "kołową ramką z prądem" jest również elektron krążący po orbicie w atomie. Moment dipolowy elektronu krążącego po orbicie o promieniu r wynosi

Natężenie prądu I wytwarzanego przez elektron o ładunku e przebiegający orbitę w czasie T (okres obiegu) wynosi

gdzie v jest prędkością elektronu. Stąd

gdzie L = mvr jest momentem pędu elektronu. Elektron, krążący po orbicie jest więc elementarnym dipolem magnetycznym. Własności magnetyczne ciał są właśnie określone przez zachowanie się tych elementarnych dipoli w polu magnetycznym. Własności te omówimy w dalszych rozdziałach.