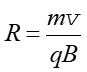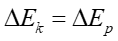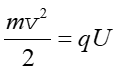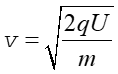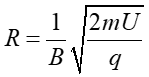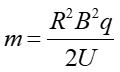Ruch naładowanych cząstek w polu magnetycznym

22.3 Ruch naładowanych cząstek w polu magnetycznym

Zauważmy, że zgodnie z równaniem (22.1) wektor siły F działającej na naładowaną cząstkę poruszającą się w polu magnetycznym jest zawsze prostopadły do wektora prędkości v i wektora B. Oznacza to, że siła F nie może zmienić wartości prędkości v, a co za tym idzie nie może zmienić energii kinetycznej cząstki. Siła F może jedynie zmienić kierunek prędkości v, zakrzywić tor jej ruchu. Siła magnetyczna jest więc siłą dośrodkową.

Żeby prześledzić tor ruchu naładowanej cząstki w polu magnetycznym rozpatrzmy cząstkę, która z prędkością v wpada do jednorodnego stałego pola magnetycznego o indukcji B tak jak na rysunku 22.5.

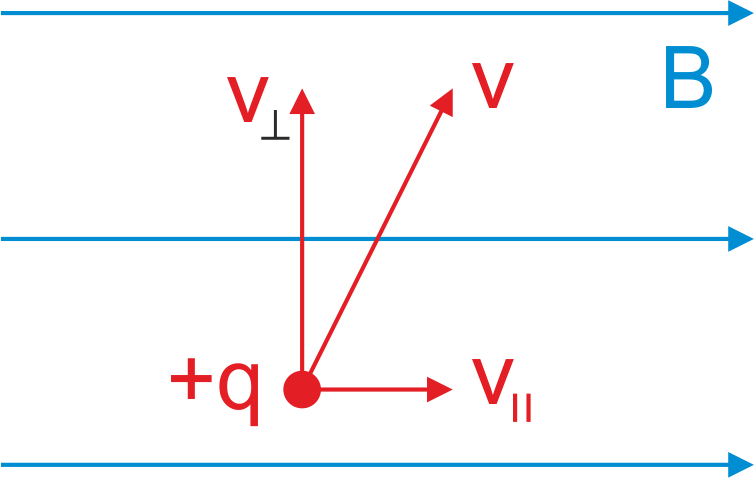
Rys. 22.5. Naładowana cząstka wpada do pola B z prędkością v

Prędkość początkową cząstki (z którą wlatuje w obszar pola B) możemy rozłożyć na dwie składowe: jedną równoległą , a drugą prostopadłą do pola B. Zauważmy, że zgodnie ze wzorem (22.2) siła magnetyczna związana jest tylko ze składową prędkości prostopadłą do pola B (θ = 90º) natomiast nie zależy od składowej równoległej do pola (θ = 0º). Siła magnetyczna zmienia więc tylko składową prędkości prostopadłą do pola B, natomiast składowa prędkości równoległa pozostaje stała.
W rezultacie cząstka przemieszcza się ze stałą prędkością wzdłuż pola B równocześnie zataczając pod wpływem siły magnetycznej okręgi w płaszczyźnie prostopadłej do pola. Cząsteczka porusza się po spirali tak jak pokazano na rysunku 22.6.

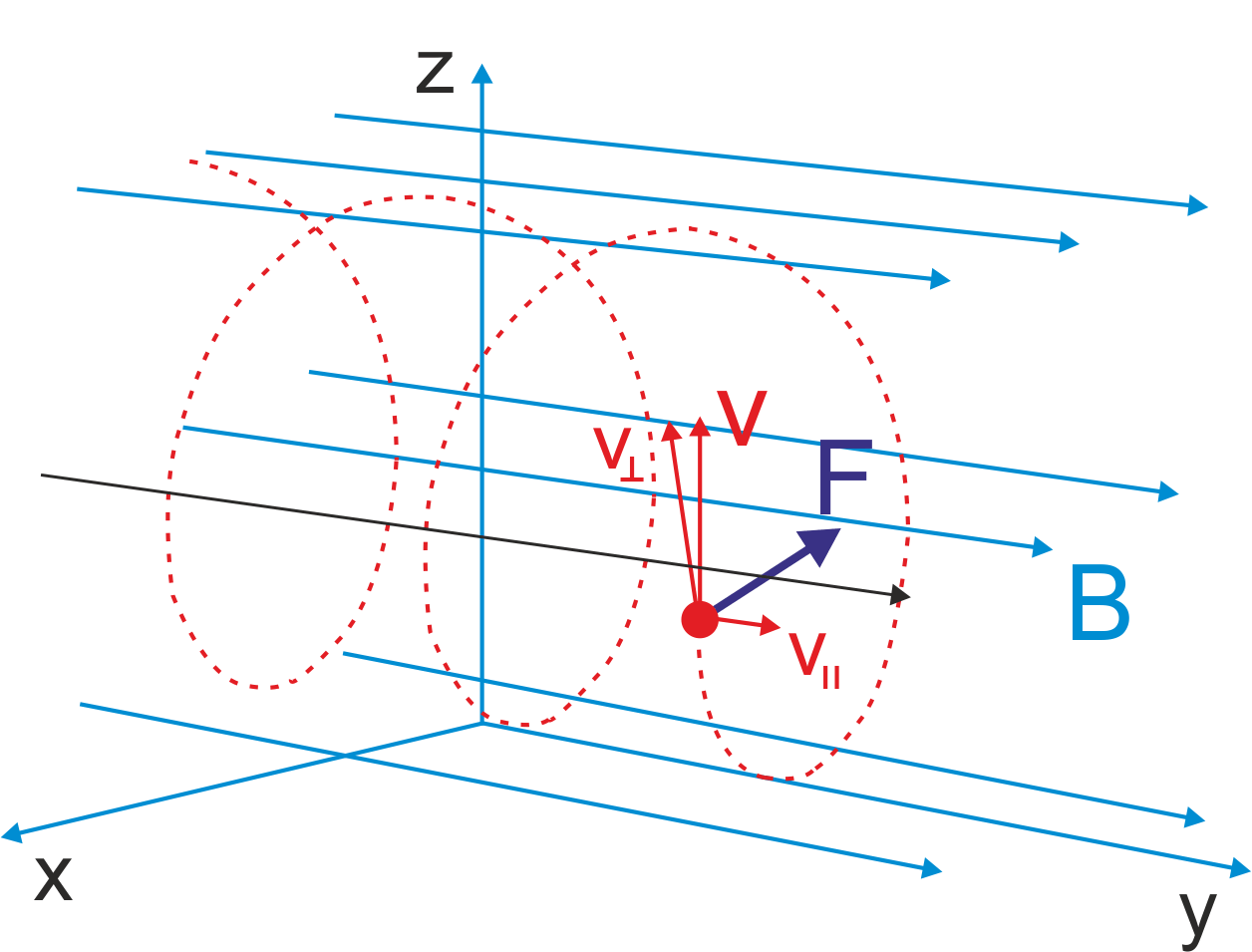
Rys. 22.6. Naładowana cząsteczka poruszająca się w polu magnetycznym po torze spiralnym

Ćwiczenie
Teraz spróbuj opisać ruch ładunku q, który porusza się z prędkością v prostopadle do pola magnetycznego B. Ponieważ prędkość jest prostopadła do pola B to tor cząstki jest okręgiem leżącym w płaszczyźnie prostopadłej do pola B. Oblicz promień tego okręgu i częstotliwość z jaką krąży ładunek. Sprawdź obliczenia i wynik.

Symulacje komputerowe
Korzystając z załączonego programu komputerowego „Tor ładunku w polu magnetycznym B”, dostępnego na stronie WWW autora i na stronie Open AGH, możesz prześledzić prześledzić tor po jakim porusza się naładowana cząstka w polu magnetycznym w zależności od wartości indukcji pola B, wartości prędkości cząstki, oraz kąta pod jakim cząstka wpada do pola B. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera.

Zjawisko odchylania toru naładowanych cząstek w polu magnetycznym znalazło szerokie zastosowanie w technice i nauce. Jednym z przykładów jest spektrometr masowy , którego schemat jest pokazany na rysunku 22.7.

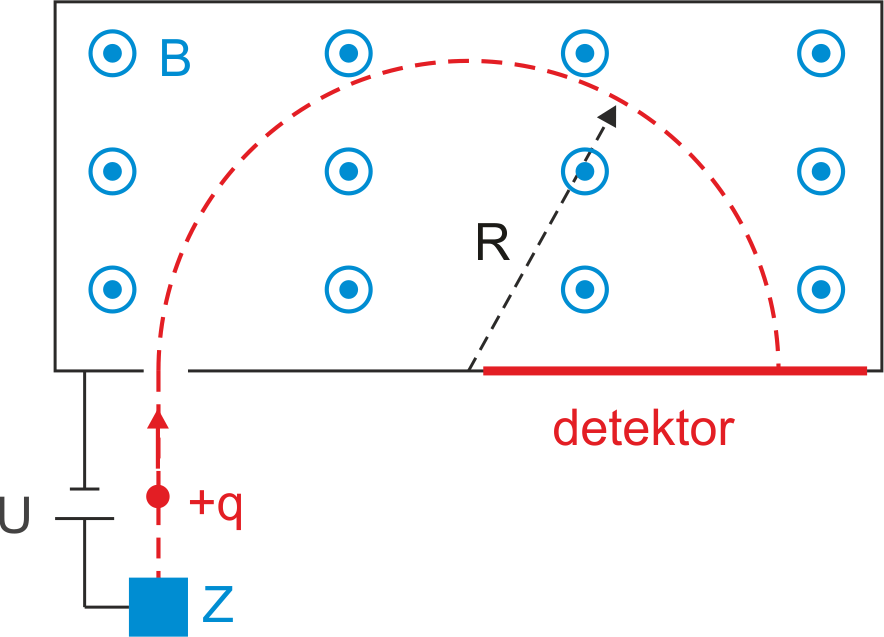
Rys. 22.7. Schemat działania spektrometru masowego

Cząstka (jon) o masie m i ładunku q wyemitowana ze źródła Z zostaje przyspieszona napięciem U po czym wlatuje w obszar jednorodnego pola magnetycznego B prostopadłego do toru cząstki. (Pamiętaj, że symbol oznacza wektor skierowany przed płaszczyznę rysunku, a symbolem oznaczamy wektor skierowany za płaszczyznę rysunku.) Pole magnetyczne zakrzywia tor cząstki, tak że porusza się ona po półokręgu o promieniu R, po czym zostaje zarejestrowana w detektorze (np. na kliszy fotograficznej) w odległości 2R od miejsca wejścia w pole magnetyczne

Promień okręgu po jakim porusza się naładowana cząstka w polu B obliczyliśmy w ostatnim ćwiczeniu

(22.3)

gdzie v jest prędkością z jaką porusza się cząstka. Tę prędkość uzyskuje ona dzięki przyłożonemu napięciu U. Zmiana energii potencjalnej ładunku przy pokonywaniu różnicy potencjału U jest równa energii kinetycznej jaką uzyskuje ładunek

(22.4)

lub

(22.5)

Stąd otrzymujemy wyrażenie na prędkość v

(22.6)

i podstawiamy je do równania 22.3

(22.7)

Ostatecznie po przekształceniu otrzymujemy

(22.8)

Widzimy, że pomiar odległości (2R), w jakiej została zarejestrowana cząstka pozwala na wyznaczenie jej masy m.

Zakrzywianie toru cząstek w polu magnetycznym jest również wykorzystywane w urządzeniach zwanych akceleratorami . Akceleratory - urządzenia służące do przyspieszania cząstek naładowanych, znalazły szerokie zastosowanie w nauce, technice i medycynie. Więcej o ...