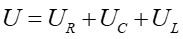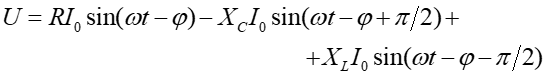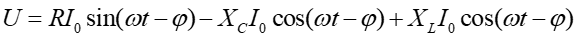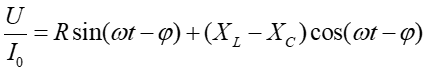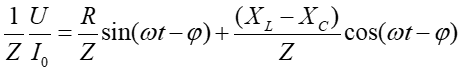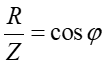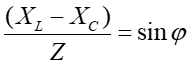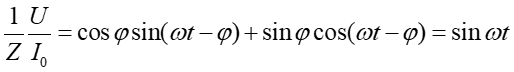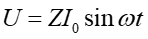Drgania w obwodzie RLCZawada w obwodzie RLC
W omawianym obwodzie RLC pomimo szeregowego połączenia oporów omowego, pojemnościowego i indukcyjnego opór zastępczy (zawada) nie jest sumą algebraiczną tych oporów. Wynika to bezpośrednio z występujących w obwodzie przesunięć fazowych pomiędzy prądem i napięciem, które trzeba uwzględniać przy dodawaniu napięć i w konsekwencji przy liczeniu zawady.
Żeby to sprawdzić obliczmy napięcie wypadkowe w obwodzie RLC
|
(1) |
Po podstawieniu odpowiednich wyrażeń i uwzględnieniu przesunięć fazowych pomiędzy prądem i napięciem dla poszczególnych elementów obwodu otrzymujemy
|
(2a) |
|
(2b) |
Zwróćmy uwagę, że na kondensatorze napięcie U pozostaje za prądem I, a na cewce U wyprzedza I.
Równanie (2b) można przekształcić do postaci
|
(3) |
Mamy więc teraz dodać do siebie dwie funkcje, sinus i cosinus.
W tym celu skorzystamy z wyrażenia (25.17), zgodnie z którym 
.
Relacja ta, pokazana na rysunku 1, przedstawia związek między
reaktancjami XL, XC oporem R oraz kątem fazowym
φ.
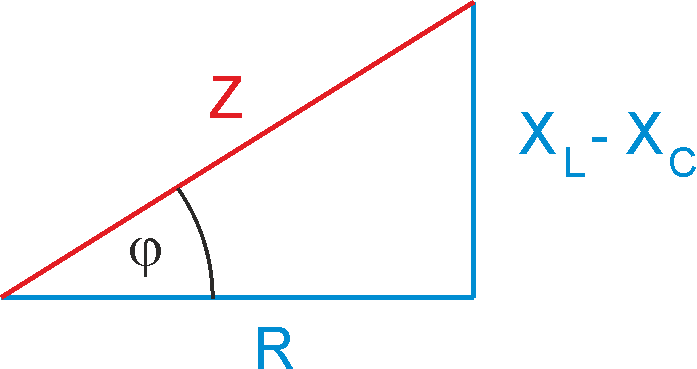
Rys. 1. Związek między reaktancjami XL, XC oporem R, zawadą Z oraz kątem fazowym φ
Zauważmy, że przeciwprostokątna trójkąta na rysunku 1 jest równa zawadzie
.
Dzielimy teraz obustronnie równanie (3) przez Z i otrzymujemy
|
(4) |
Zgodnie z rysunkiem 1
|
(5) |
|
(6) |
Tak więc ostatecznie
|
(7) |
Otrzymaliśmy ponownie relację
|
(8) |
z której wynika, że napięcie U wyprzedza prąd 
o kąt fazowy φ oraz,
że zawada Z jest stałą proporcjonalności pomiędzy U0 i I0.