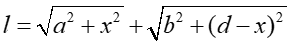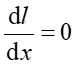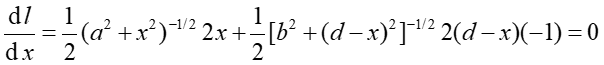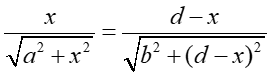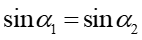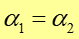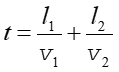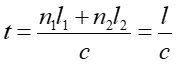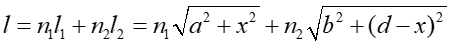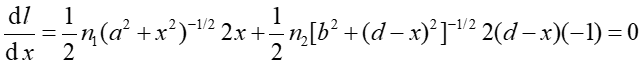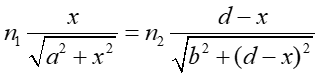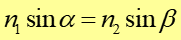Zasada Fermata

Zasadę Fermata formułujemy w następujący sposób

Prawo, zasada, twierdzenie
Promień świetlny biegnący z jednego punktu do drugiego przebywa drogę, na której przebycie trzeba zużyć w porównaniu z innymi, sąsiednimi drogami, minimum albo maksimum czasu.

Zasada ta wyjaśnia prostoliniowy bieg światła w ośrodku jednorodnym bo linia prosta odpowiada minimum drogi, a tym samym i minimum czasu. Właśnie z tej zasady można wyprowadzić prawa odbicia i załamania.

Na rysunku 1 są przedstawione dwa punkty A i B oraz łączący je promień APB, który odbija się od powierzchni granicznej w punkcie P.

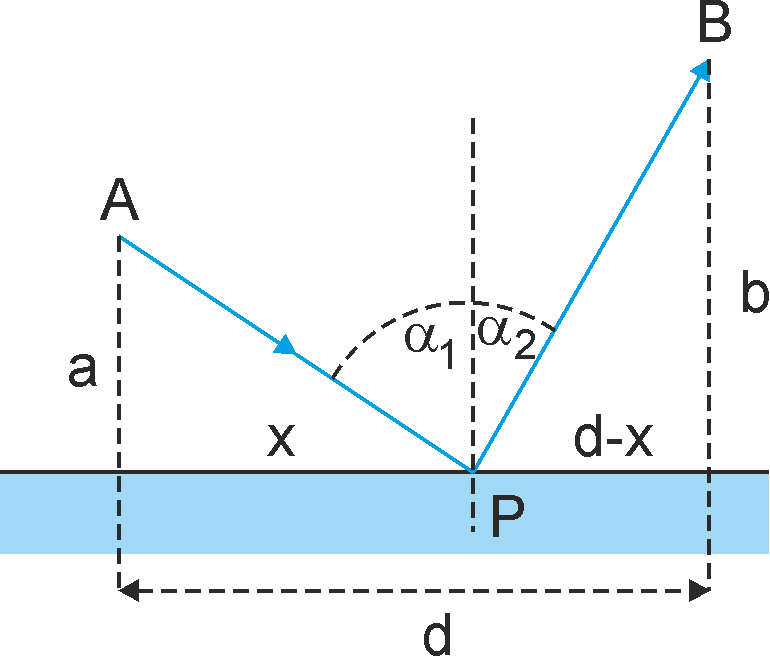
Rys. 1. Promień wychodzący z punktu A po odbiciu w punkcie P trafia do punktu B

Całkowita długość drogi promienia wynosi

(1)

gdzie x jest zmienną zależną od położenia punktu P (punkt odbicia promienia).

Zgodnie z zasadą Fermata punkt P (zmienną x) wybieramy tak, żeby czas przebycia drogi APB był minimalny (lub maksymalny, lub niezmieniony). Matematycznie oznacza to warunek

(2)

więc otrzymujemy

(3)

a po przekształceniu

(4)

Porównując z rysunkiem 1 widzimy, że jest to równoważne zapisowi

(5)

lub

(6)

co wyraża prawo odbicia.

Podobnie postępujemy w celu wyprowadzenia prawa załamania. Rozpatrzmy sytuację przedstawioną na rysunku 2.

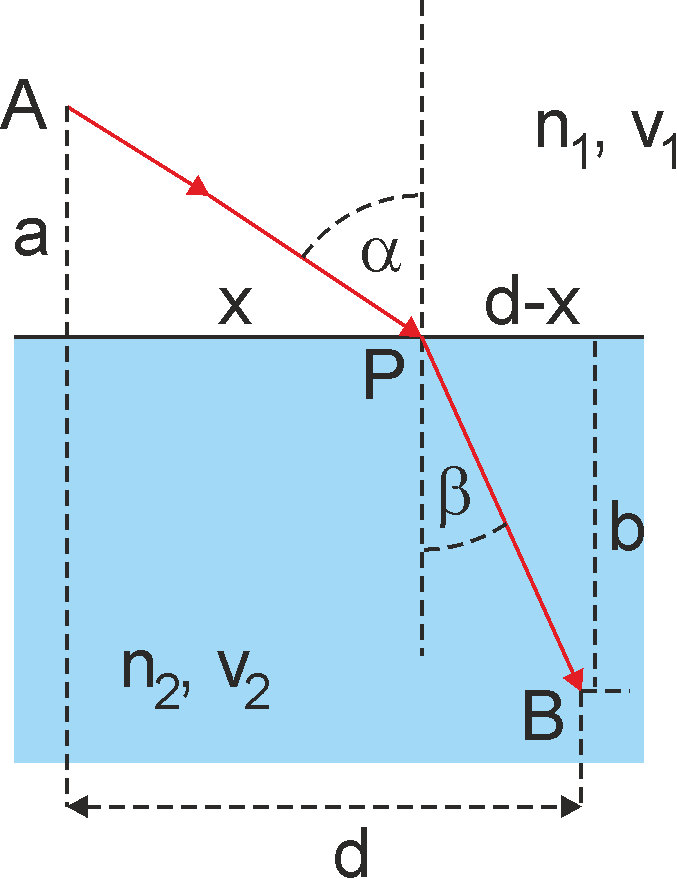
Rys. 2. Promień wychodzący z punktu A po załamaniu w punkcie P na granicy ośrodków trafia do punktu B

Czas przelotu z A do B przez punkt P jest dany jest wzorem

(7)

Uwzględniając, że n = c/v możemy przepisać to równanie w postaci

(8)

Wyrażenie w liczniku jest drogą optyczną promienia. Ponownie dobieramy zmienną x (położenie punktu P), tak aby droga l była minimalna czyli, aby dl/dx = 0. Ponieważ droga optyczna jest równa

(9)

więc otrzymujemy

(10)

a po przekształceniu

(11)

Porównując ten wynik z rysunkiem 2 otrzymujemy

<12)

co jest prawem załamania.