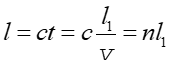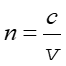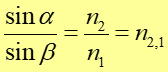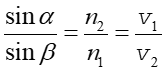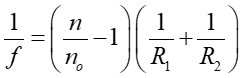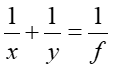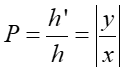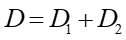28.2 Odbicie i załamanie
Współczynnik załamania, droga optyczna, dyspersja światła
Wiemy już, że światło rozchodzi się w próżni z prędkością c. Natomiast, jak pokazują wyniki doświadczeń, w ośrodkach materialnych prędkość światła jest mniejsza. Jeżeli w jednorodnym ośrodku światło przebędzie w czasie t drogę l1 = vt to droga l jaką w tym samym czasie światło przebyłoby w próżni wynosi
|
(28.1) |
|
(28.2) |
nosi nazwę bezwzględnego współczynnika załamania
![]() . Natomiast iloczyn drogi geometrycznej
l1
i współczynnika załamania n nosi nazwę drogi
optycznej
. Natomiast iloczyn drogi geometrycznej
l1
i współczynnika załamania n nosi nazwę drogi
optycznej ![]() .
Poniżej w tabeli 28.1 podane zostały bezwzględne współczynniki załamania wybranych substancji.
.
Poniżej w tabeli 28.1 podane zostały bezwzględne współczynniki załamania wybranych substancji.
Tab. 28.1. Bezwzględne współczynniki załamania wybranych ośrodków (dla λ = 589 nm - żółte światło sodu)
| Ośrodek | Współczynnik załamania |
|---|---|
| powietrze | 1.003 |
| woda | 1.33 |
| alkohol etylowy | 1.36 |
| kwarc | 1.46 |
| szkło zwykłe | 1.52 |
| polietylen | 1.52 |
| szafir | 1.77 |
| diament | 2.42 |
W nagłówku powyższej tabeli podano dla jakiej fali zostały wyznaczone współczynniki załamania.
Jest to ważna informacja bo, jak pokazuje doświadczenie, prędkość
fali przechodzącej przez ośrodek zależy od częstotliwości światła.
Zjawisko to nazywamy dyspersją światła
![]() .
Dla większości materiałów obserwujemy, że wraz ze wzrostem częstotliwości
fali świetlnej maleje jej prędkość czyli rośnie współczynnik załamania (rys. 28.2).
.
Dla większości materiałów obserwujemy, że wraz ze wzrostem częstotliwości
fali świetlnej maleje jej prędkość czyli rośnie współczynnik załamania (rys. 28.2).
Prawo odbicia i prawo załamania
Jeżeli światło pada na granicę dwóch ośrodków to ulega zarówno odbiciu na powierzchni granicznej jak i załamaniu przy przejściu do drugiego ośrodka tak jak pokazano to na rysunku 28.2 dla powierzchni płaskiej.
Na rysunku pokazana jest też dyspersja światła; promień niebieski jest bardziej załamany niż
czerwony. Światło białe, złożone z fal o wszystkich długościach z zakresu widzialnego, uległo
rozszczepieniu ![]() to jest rozdzieleniu na barwy składowe. Na rysunku pokazano promienie świetlne
tylko dla dwu skrajnych barw niebieskiej i czerwonej.
to jest rozdzieleniu na barwy składowe. Na rysunku pokazano promienie świetlne
tylko dla dwu skrajnych barw niebieskiej i czerwonej.
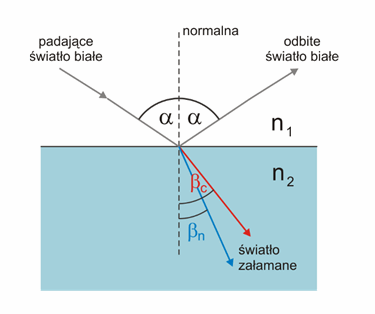
Rys. 28.2. Odbicie i załamanie światła białego na granicy dwóch ośrodków (n2 > n1)
Odbiciem i załamaniem rządzą dwa następujące prawa
|
Prawo, zasada, twierdzenie Prawo odbicia: Promień padający, promień odbity i normalna do powierzchni granicznej wystawiona w punkcie padania promienia leżą w jednej płaszczyźnie i kąt padania równa się kątowi odbicia α1 = α2. |
|
Prawo, zasada, twierdzenie Prawo załamania: Stosunek sinusa kata padania do sinusa kąta załamania jest równy stosunkowi bezwzględnego współczynnika załamania ośrodka drugiego n2 do bezwzględnego współczynnika załamania ośrodka pierwszego n1, czyli współczynnikowi względnemu |
|
(28.3) |
|
(28.4) |
gdzie skorzystaliśmy z definicji bezwzględnego współczynnika załamania
![]() .
.
Powyższe prawa dotyczące fal elektromagnetycznych można wyprowadzić z równań Maxwella, ale jest to matematycznie trudne. Można też skorzystać z prostej (ale ważnej) zasady odkrytej w XVII w. przez Fermata Więcej o ... .
Z prawa załamania (wzór 28.3) wynika, że gdy promień świetlny przechodzi z ośrodka gęstszego optycznie do ośrodka rzadszego,
np. z wody do powietrza, to kąt załamania promienia jest większy od kąta padania:
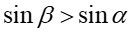 ,
bo n2 < n1. Wynika stąd, że istnieje taki graniczny kąt padania
αgr, przy którym kąt załamania
β= 90º
i promień załamany biegnie wzdłuż granicy ośrodków. Natomiast dla kąta padania
α > αgr,
promień nie ulega załamaniu tylko odbija się od granicy ośrodków (rysunek poniżej).
Zjawisko to nosi nazwę całkowitego wewnętrznego odbicia . Zjawisko całkowitego wewnętrznego odbicia wykorzystywane
jest między innymi w pryzmatach całkowitego odbicia w aparatach fotograficznych, lornetkach oraz światłowodach.
,
bo n2 < n1. Wynika stąd, że istnieje taki graniczny kąt padania
αgr, przy którym kąt załamania
β= 90º
i promień załamany biegnie wzdłuż granicy ośrodków. Natomiast dla kąta padania
α > αgr,
promień nie ulega załamaniu tylko odbija się od granicy ośrodków (rysunek poniżej).
Zjawisko to nosi nazwę całkowitego wewnętrznego odbicia . Zjawisko całkowitego wewnętrznego odbicia wykorzystywane
jest między innymi w pryzmatach całkowitego odbicia w aparatach fotograficznych, lornetkach oraz światłowodach.
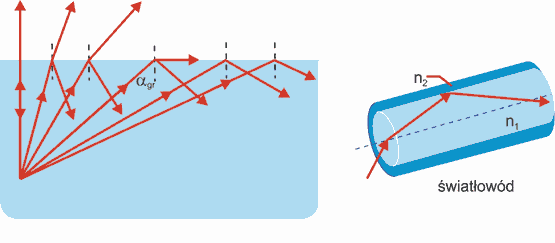
Rys. 28.3. Całkowite wewnętrzne odbicie na granicy dwóch ośrodków (n2 < n1)
|
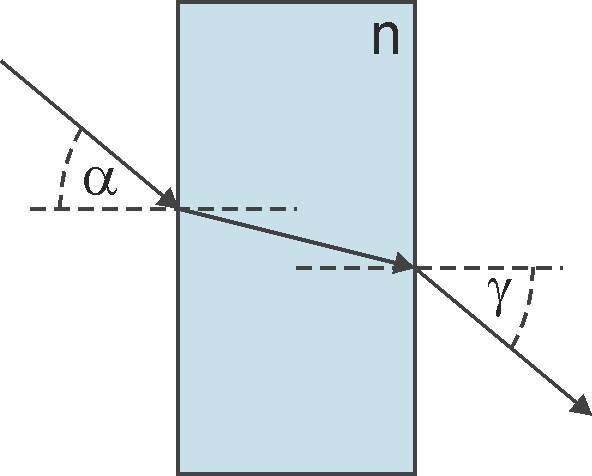
Ćwiczenie Spróbuj teraz prześledzić bieg promienia świetlnego padającego pod katem α na umieszczoną w powietrzu prostopadłościenną szklaną płytkę wykonaną ze szkła o współczynniku załamania n tak jak pokazano na rysunku poniżej. Korzystając z prawa załamania oblicz kąt γ pod jakim promień opuszcza płytkę. Sprawdź obliczenia i wynik. |
|
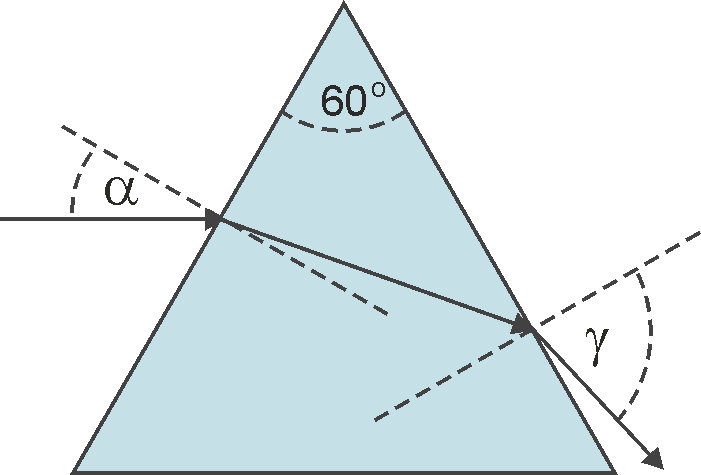
Ćwiczenie Podobnie jak w poprzednim ćwiczeniu, promień światła załamuje się dwukrotnie tym razem przechodzący przez równoboczny pryzmat, pokazany na rysunku poniżej. Promień biegnie początkowo równolegle do podstawy pryzmatu, a opuszcza go pod katem γ. Oblicz ten kąt wiedząc, że pryzmat jest wykonany z materiału o współczynniku załamania n = 1.5. Sprawdź obliczenia i wynik. |
Omawiając odbicie i załamanie ograniczyliśmy się do fal płaskich i do płaskich
powierzchni. Uzyskane wyniki stosują się jednak do bardziej ogólnego
przypadku fal kulistych. Stosują się również do kulistych
powierzchni odbijających - zwierciadeł
kulistych ![]() i kulistych powierzchni załamujących - soczewek
i kulistych powierzchni załamujących - soczewek
![]() . Te ostatnie mają
szczególne znaczenie ze względu na to, że stanowią część układu
optycznego oka i wielu przyrządów optycznych takich jak np. lupa, teleskop, mikroskop.
. Te ostatnie mają
szczególne znaczenie ze względu na to, że stanowią część układu
optycznego oka i wielu przyrządów optycznych takich jak np. lupa, teleskop, mikroskop.
Soczewki
Soczewkami nazywamy ciała przeźroczyste ograniczone dwoma powierzchniami o promieniach krzywizn R1 i R2.
Nasze rozważania własności optycznych soczewek ograniczymy do soczewek
cienkich tzn. takich, których grubość jest znacznie mniejsza od
promieni krzywizn R1 i R2
powierzchni ograniczających soczewkę. Ponadto zakładamy, że
promienie świetlne padające na soczewkę tworzą małe kąty z osią
soczewki tj. prostą przechodząca przez środki krzywizn obu
powierzchni. Takie promienie (prawie prostopadłe do powierzchni
soczewki) leżące w pobliżu osi soczewki nazywamy promieniami
przyosiowymi ![]() .
Z wyjątkiem promienia biegnącego wzdłuż osi soczewki, każdy promień przechodzący
przez soczewkę ulega dwukrotnemu załamaniu na obu powierzchniach soczewki.
.
Z wyjątkiem promienia biegnącego wzdłuż osi soczewki, każdy promień przechodzący
przez soczewkę ulega dwukrotnemu załamaniu na obu powierzchniach soczewki.
Jeżeli przy przejściu przez soczewkę promienie równoległe do osi soczewki
zostają odchylone w stronę tej osi to soczewkę nazywamy skupiającą
![]() , a jeżeli odchylają
się od osi, soczewka jest rozpraszająca
, a jeżeli odchylają
się od osi, soczewka jest rozpraszająca
![]() . Soczewka skupiająca
odchyla promienie równoległe w taki sposób, że są one skupiane w punkcie F, w odległości f od soczewki. Punkt F
nosi nazwę ogniska, a odległość f nazywamy ogniskową soczewki
. Soczewka skupiająca
odchyla promienie równoległe w taki sposób, że są one skupiane w punkcie F, w odległości f od soczewki. Punkt F
nosi nazwę ogniska, a odległość f nazywamy ogniskową soczewki
![]() .
.
Na rysunku 28.3 pokazany jest sposób wyznaczania położenia obrazu
przedmiotu rozciągłego (strzałki). W celu jego wyznaczenia rysujemy
promień równoległy do osi soczewki. Promień ten po przejściu przez
soczewkę przechodzi przez ognisko F. Drugi promień przechodzi
przez środek soczewki i nie zmienia swojego kierunku. Jeżeli obraz
powstaje w wyniku przecięcia się tych promieni, to taki obraz nazywamy
rzeczywistym ![]() (rysunek 28.3a). Natomiast gdy promienie po przejściu przez soczewkę są rozbieżne to obraz otrzymujemy
z przecięcia się promieni przedłużonych i taki obraz nazywamy
pozornym
(rysunek 28.3a). Natomiast gdy promienie po przejściu przez soczewkę są rozbieżne to obraz otrzymujemy
z przecięcia się promieni przedłużonych i taki obraz nazywamy
pozornym ![]() (rysunek 26.3 b).
(rysunek 26.3 b).
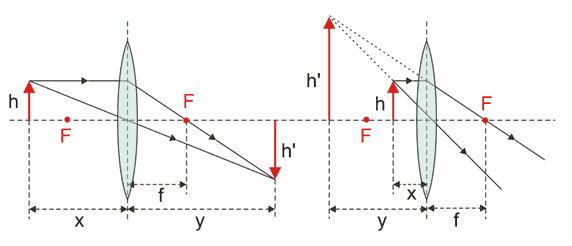
Rys. 28.4. Powstawanie obrazu w soczewce skupiającej: a) rzeczywistego, b) pozornego
Bieg promienia świetlnego w soczewce zależy od kształtu soczewki tzn. od R1 i R2, od współczynnika załamania n materiału z jakiego wykonano soczewkę oraz od współczynnika załamania no ośrodka, w którym umieszczono soczewkę. Ogniskowa soczewki jest dana równaniem
|
(28.5) |
Przy opisie soczewek przyjmujemy konwencję, że promienie krzywizn wypukłych powierzchni są wielkościami dodatnimi, a promienie krzywizn wklęsłych powierzchni są wielkościami ujemnymi; powierzchni płaskiej przypisujemy nieskończony promień krzywizny.
Gdy ogniskowa jest dodatnia f > 0 to soczewka jest skupiająca, a gdy f < 0 to soczewka jest rozpraszająca.
Odległość x przedmiotu od soczewki i odległość y obrazu od soczewki (rysunek 28.3) są powiązane równaniem dla cienkich soczewek
|
(28.6) |
a powiększenie liniowe obrazu jest dane wyrażeniem
|
(28.7) |
Przyjmuje się umowę, że odległości obrazów pozornych od soczewki są ujemne.
|
Symulacje komputerowe Możesz prześledzić geometryczną metodę wyznaczania obrazu wytwarzanego przez soczewkę skupiającą i rozpraszającą korzystając z programu komputerowego „Soczewki”, dostępnego na stronie WWW autora i na stronie Open AGH. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera. |
Odwrotność ogniskowej soczewki D = 1/f nazywamy zdolnością
zbierającą soczewki ![]() .
.
|
Jednostki Jednostką zdolności zbierającej soczewki jest dioptria (D); 1 D = 1/m. |
Dla układu blisko siebie leżących soczewek ich zdolności skupiające dodają się
|
(28.8) |
Wszystkie powyżej podane związki są prawdziwe dla cienkich soczewek i dla promieni przyosiowych. Tymczasem dla soczewek w rzeczywistych układach optycznych mamy do czynienia z aberracjami tj. ze zjawiskami zniekształcającymi obrazy i pogarszającymi ich ostrość.
Przykładem takiego zjawiska jest aberracja sferyczna
![]() .
Polega ona na tym, że w miarę oddalania się od osi zwierciadła
promienie zaczynają odchylać się od ogniska. W ten sposób zamiast
otrzymać obraz punktowy (jak dla promieni przyosiowych) otrzymujemy
obraz rozciągły (plamkę). Inną wadą soczewek jest aberracja
chromatyczna
.
Polega ona na tym, że w miarę oddalania się od osi zwierciadła
promienie zaczynają odchylać się od ogniska. W ten sposób zamiast
otrzymać obraz punktowy (jak dla promieni przyosiowych) otrzymujemy
obraz rozciągły (plamkę). Inną wadą soczewek jest aberracja
chromatyczna ![]() .
Jest ona związana ze zjawiskiem dyspersji. Światło o różnych
barwach (różnych częstotliwościach) ma różne prędkości, więc i
różne współczynniki załamania w szkle, z którego zrobiono soczewkę.
W konsekwencji różne barwy są różnie ogniskowane i obraz białego punktu jest barwny.
.
Jest ona związana ze zjawiskiem dyspersji. Światło o różnych
barwach (różnych częstotliwościach) ma różne prędkości, więc i
różne współczynniki załamania w szkle, z którego zrobiono soczewkę.
W konsekwencji różne barwy są różnie ogniskowane i obraz białego punktu jest barwny.
Te jak i jeszcze inne wady soczewek można korygować stosując zestawy soczewek oraz wykonując soczewki o odpowiednich krzywiznach i z materiału o odpowiednim współczynniku załamania.


 Odbicie i załamanie
Odbicie i załamanie